Not a harmonic mean question
Let x , y , z ≥ 0 be reals such that x + y + z = 1 . Find the maximum possible value of
x ( x + y ) 2 ( y + z ) 3 ( x + z ) 4 .
The answer is 0.015625.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
9 solutions
Beautifully Awesome Solution!! @shubhendra singh +1!!
Log in to reply
Thanks ! But I think @Joel Tan deserves more credit for such amazing problem.
It is necessary to state an equality case.
Log in to reply
AM-GM reaches equality with all addends in the sum equal, particularly x = 1 − z = 1 − x = 2 1 − y . x = 1 − x gives x = 2 1 , then x = 1 − z gives z = 2 1 , and finally this leaves y = 0 .
I have mentioned it , thanks.
awesome solution really!!!
Pro pro. I wished I can think of this solution myself, but I didn't.
As I was unfamiliar with the actual techniques involved, I went at it algebraically. I wouldn't recommend it. It was gross. I did get the correct answer, though.
● z=1-x-y, x (x+y)^2 (y+z)^3 (x+z)^4
● maximum {-(x-1)^3 x (y-1)^4 (x+y)^2}
● 1÷64 @ (x,y) = (.5, 0)
Wolframalpha
How this idea of dividing (1-y) by 2 came to yur mind????....
Since (x+z) has greatest power therfore it should be more closer to 1....so I tried (x+z)=1....and solved for it.... And got it correct. ☺
i guessed the answeer first try but messed up the computation
@shubhendra singh Please explain,
W h y x + 3 ( 1 − x ) i n s t e a d o f a n y o t h e r a x + 3 ( 1 − x ) 3 a ( 1 + 2 a ) ?
Log in to reply
For equality to exist a x = 3 a ( 1 − x ) ( 1 + 2 a ) = 1 − z = 2 1 − y
On solving we get x = 4 + 2 a 1 + 2 a y = a − 3 a − 1 z = a − 3 a − 2 and x + y + z = 1
By doing all this we finally get a equation which is 4 a 2 − a − 3 = 0 this gives a = 1 , 4 − 3
Since a can't be negative we get a=1.
Sorry for the late reply.
Can you explain why we apply the AM-GM inequality in that particular way with those coefficients? And also why do we take 4(1-y) /2?
Log in to reply
@Harsh Khatri , you asked this some time ago, but I don't see a response anywhere. Using x+y+z=1 to substitute (1-z) for (x+y), etc, makes it so that each factor only involves one variable, making it easier to adjust how many of each variable is represented in the arithmetic mean, so that there are the same number of each and the x+y+z=1 can be substituted in. Selecting (1-y)/2 makes the coefficients of x, y, and z match up in the AM, allowing the substitution. In essence, @Shubhendra Singh has taken the AM and GM of the sequence {x, (1-z), (1-z), (1-x), (1-x), (1-x), (1-y)/2, (1-z)/2, (1-y)/2, (1-y)/2}. That is where the 4(1-y)/2 comes from in the AM.
It seems this AM-GM method in general only results in an upper bound, unless equality can be shown. In this problem, equality is fairly straightforward to show, but in other similar problems, it can be more challenging.
I had a different approach...
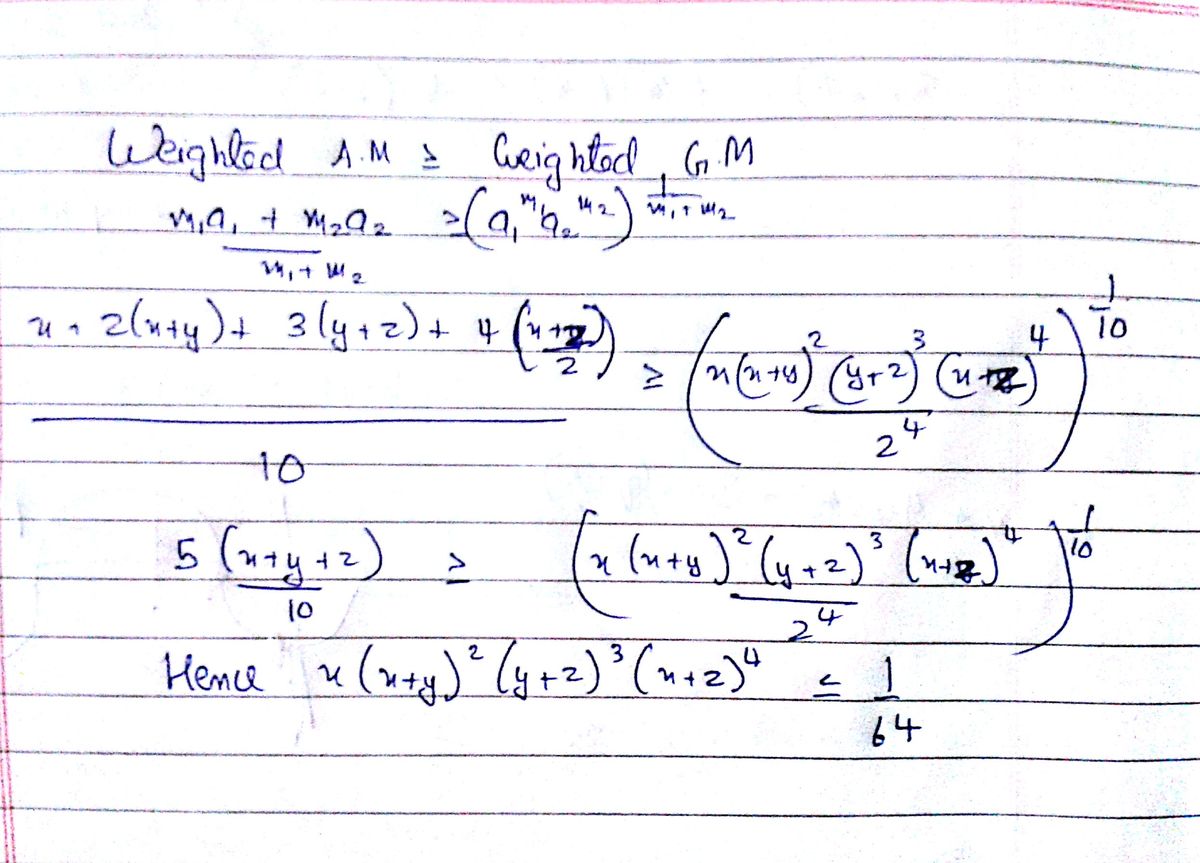
How the idea of dividing by 2 came to ur mind????
First note that
x + y = 1 − z
y + z = 1 − x
x + z = 1 − y .
Then let
f ( x , y , z ) = x ( 1 − z ) 2 ( 1 − x ) 3 ( 1 − y ) 4
If x , y , and z are optimized such that f ( x , y , z ) is maximized, then we claim y is the least of the variables.
If z ≤ y , then 1 − y ≤ 1 − z . Thus,
f ( x , y , z ) ≤ f ( x , z , y ) .
So interchanging y and z yields a greater solutions, so we may assume y ≤ z .
Similarly, if x ≤ y , then 1 − y ≤ 1 − x . Thus,
f ( x , y , z ) ≤ f ( y , x , z ) .
So interchanging x and y yields a greater solution, so again, we may assume y ≤ x .
Now to optimize f , clearly we can choose y = 0 . Thus, since x + y + z = x + z = 1 , we can replace 1 − z in f with x , giving us
f ( x ) = x 3 ( 1 − x ) 3 .
We then use calculus. We have that
f ′ ( x ) = 3 x 2 ( 1 − x ) 3 − 3 x 3 ( 1 − x ) 2 = 3 x 2 ( 1 − x ) 2 ( 1 − 2 x )
which has critical points 0 , 1 / 2 , and 1 . Since f ( 1 ) = f ( 0 ) = 0 , the maximized value is f ( 1 / 2 ) = 1 / 6 4 .
Loved your method! Is there any formal name to it? I would like to see some more uses of it!
Log in to reply
I have no idea, I just made it up as I went. Back then, my algebra techniques weren't as strong, so I used my calculus skills instead.
Well, my way is a bit more intuitive and don't know if it is a demonstration... you first have x+y = 1-z, y+z=1-x, x+z=1-y. From here, you substitute this on the equation and see what's the strongest. (1-y)^4 is indeed the strongest, so you will intuitively know that you have to make y as small as possible (so y=0). You then obtain the equation (x*z)^3. The maximum value is reached when x=z=1/2 (you know that there is only one value possible as solution since the checkbox only accept one answer, and because there is a symmetry between x and z, you can also find out that x=z) So you get x=y=1/2, z=0 and you can then answer!
Let z = 1 − x − y , take the partial derivatives of the function, set them equal to 0, solve one of them for y , plug in why into they other equation to get x , use x to find y and z , and finally plug them into the original equation to get 6 4 1 , giving us our final answer of p + q = 1 + 6 4 = 6 5
P.S. (Sorry if the picture is sideways to you)
Fantastic solutions above. I went about this in a little bit different way. From the equation we know the biggest x+y, y+z, or x+z can be is 1. If one of these terms is 1 then the others must be less than one. Since these terms are positive and less than one the higher their order the lower their value. To maximize our value we should make x+z=1, which implies y=0. Simplifying the expression leaves us with (xz)^3 to maximize or just xz. Solving in terms of x gives us x-x^2. Finding the maxima of this give us x = 1/2 which means z = 1/2. Substituting gives us (1/2)^6 = 1/64. Thus p+q = 65.
I too have used same method
"the higher their order the lower their value"; this is all we really need to solve this. Both x and z are 7th order whereas y is only 5th. So y=0 and x=z=1/2 and substituting gives the answer.
Use A. M. - G. M. on x, x + y, x + y, y + z , y + z, y + z, and 0.5 x + 0.5 y four times. A. M. of these 10 is 0.5 which is the maximum value of tenth root of the product. Simply solving this gives the required expression to have a maximum value 1/64.
Where does the .5 come from in the last term that's included four times? Why not 4(1-y) ?
I decided that since the 4th power is the highest so I should maximize that one by making x+z=1 and y=0, then the expression becomes (x^3)(z^3), given x+z=1, I know from past experience, is maximized by setting x=1/2. You can prove this by inserting z=1-x and differentiating. So we have (1/2)^6
shubhendra singh solution - actually there are many ways to choose a,b,c,d such that a x+b (1-z)+c (1-x)+d(1-z)=k (x+y+z). But the important factor lies in the satisfiability of the equation which can be acheived only by checking equality condition. Here goes more rigorous proof of how to get to the values of a=1,b=2,c=3,d=2. Firstly the coefficients of x,y,z in the LHS of the above stated equation must be equal. This gives b=d and a+b=c. Now the other condition is that the AM-GM inequality must be satisfiable. So, we get 3 equations which must be consistent . They are :- a x=(b/2) (x+y) - (eq1) a x=(d/4) (x+z) - (eq2) a x=(c/3) (y+z) - (eq3) Finding values of y and z in terms of x from eq1 and eq2 and substituting in eq3 leads us to (2 a)/b+(4 a)/d=2+(3 a)/c Now putting b=d we get (6 a)/b=2+(3 a)/c Now putting a=c-b we get 6 c c-11 b c+3 b b=0 Solving this we get b=3 c and 2 c=3 b b=3 c could be ruled out as substituting this in a+b=c leads to a=-2 c which means either a or c is negative which is not desirable. So we take 2 c=3 b so we put c=3, b=2 From these two values d=2 as (b=d) and a=1 as (a=c-b) So this is how we could arrive at correct values of a,b,c,d which fit into all the conditions
Why are the solutions dividing by 2 when turning x+z into 1-y? The AM should be [x + 2(1-z) + 3(1-x) + 4(1-y)] / 10 based on the last term being (x+z)^4 right?
Since x + y + z = 1
So we need to find the maximum possible value of
x ( 1 − z ) 2 ( 1 − x ) 3 ( 1 − y ) 4
Apply A M ≥ G M in the following way.
1 0 x + 2 ( 1 − z ) + 3 ( 1 − x ) + 4 2 ( 1 − y ) ≥ 1 0 1 6 x ( 1 − z ) 2 ( 1 − x ) 3 ( 1 − y ) 4
1 0 7 − 2 ( x + y + z ) ≥ 1 0 1 6 x ( 1 − z ) 2 ( 1 − x ) 3 ( 1 − y ) 4
This finally gives x ( 1 − z ) 2 ( 1 − x ) 3 ( 1 − y ) 4 ≤ 2 4 × ( 2 1 ) 1 0
So the max value of x ( x + y ) 2 ( y + z ) 3 ( x + z ) 4 is 2 6 1 = 6 4 1
Equality holds when x = z = 2 1 and y = 0