Creepy Oscillations (Part 1)
Consider the scenario presented in the picture.
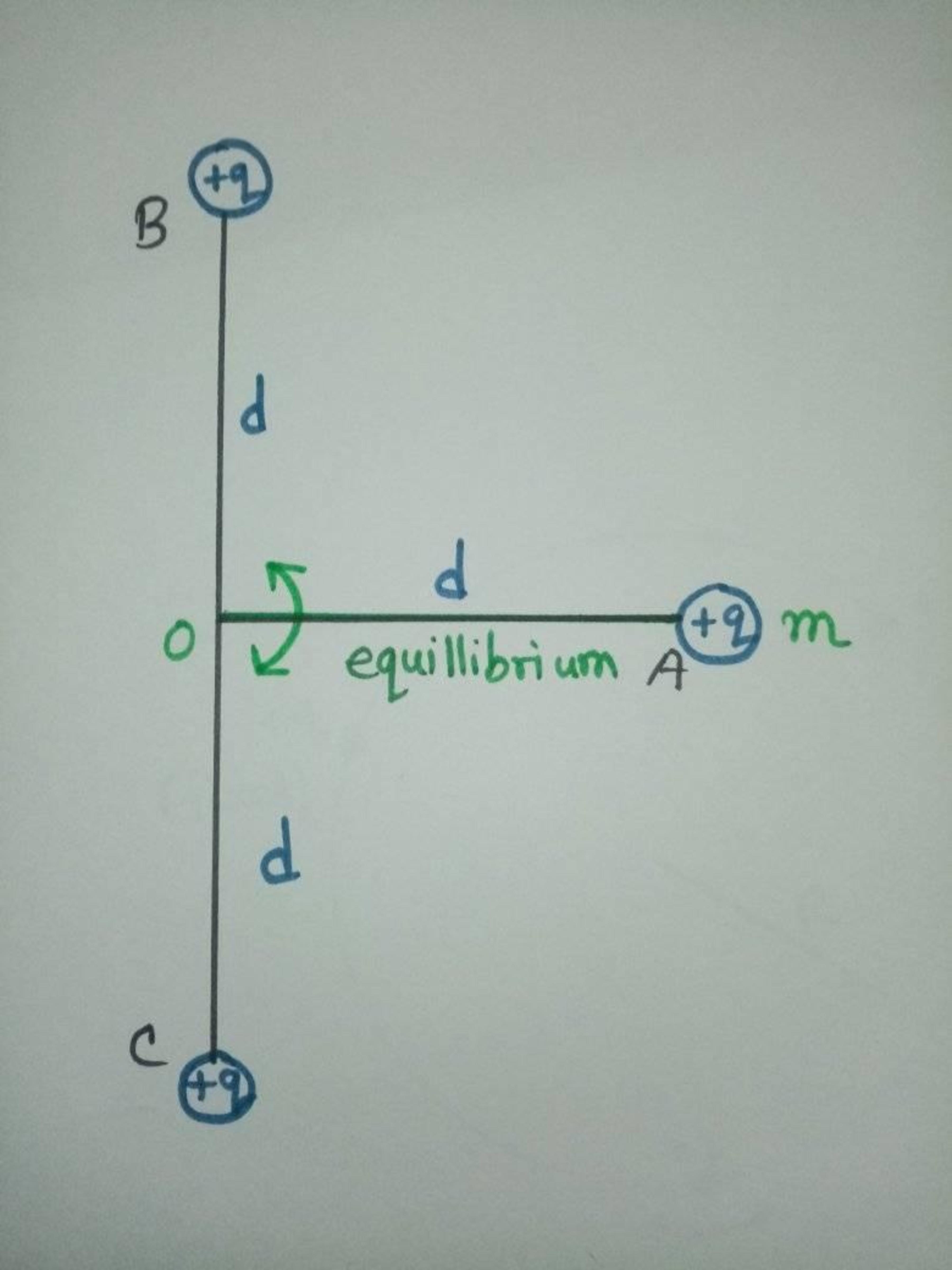
The rigid massless rod OA is holding a point charge of mass on its vertex. The rod is free to rotate around the fixed point O. And there are two more point charges( each being ) at points B and C. Each of them is fixed in its position. The separations .Not to mention, the system is in equilibrium in the shown situation.
Now, let's say we slightly displace the rod (i.e.- we rotate it through a very small angle ). What will be frequency of the resultant oscillation?
Values and Assumptions:
1) Here , ,
2) Coulomb Constant =
3) Neglect the gravitation acceleration . [Assume the process is carried out in vacuum]
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Nice problem!
At any general time t , the rod O A makes an angle θ with the horizontal. The coordinates of the point A are ( cos θ , sin θ ) .
Calculating the potential energy of the system of charges:
V = 2 K q 2 + cos 2 θ + ( 1 − sin θ ) 2 K q 2 + cos 2 θ + ( 1 + sin θ ) 2 K q 2 ⟹ V = 2 K q 2 + 2 ( 1 − sin θ ) K q 2 + 2 ( 1 + sin θ ) K q 2
The velocity components of the charge at A is ( − θ ˙ sin θ , θ ˙ cos θ ) . Therefore, the kinetic energy is:
T = 2 m θ ˙ 2
Now, since there are no dissipative forces acting on the system, its energy is conserved. This means:
E = V + T
E is a constant. Now, differentiating both sides with respect to time gives:
0 = d t d T + d t d V
⟹ θ ˙ ( m θ ¨ + 2 2 K q 2 cos θ ( ( 1 − sin θ ) − 3 / 2 − ( 1 + sin θ ) − 3 / 2 ) ) = 0
Now θ ˙ = 0 otherwise the system would not be in motion. Therefore:
m θ ¨ + 2 2 K q 2 cos θ ( ( 1 − sin θ ) − 3 / 2 − ( 1 + sin θ ) − 3 / 2 ) = 0
We are asked to analyse small oscillations. In this event, we assume sin θ ≈ θ and cos θ ≈ 1 . This transforms the equation of motion to:
m θ ¨ + 2 2 K q 2 ( ( 1 − θ ) − 3 / 2 − ( 1 + θ ) − 3 / 2 ) = 0
By doing a binomial expansion and neglecting terms of higher powers since θ is small leads to:
m θ ¨ + 2 2 K q 2 ( 1 + 2 3 θ − 1 + 2 3 θ ) = 0 m θ ¨ + 2 2 3 K q 2 θ = 0
This equation represents a simple harmonic oscillation of natural angular frequency:
ω 2 = 2 m 2 3 K q 2 ⟹ ω = 2 m 2 3 K q 2 ⟹ 2 π f = 2 m 2 3 K q 2 ⟹ f = 2 π 1 2 m 2 3 K q 2