Creepy Oscillations (Part 3)
Consider the scenario presented in the picture.
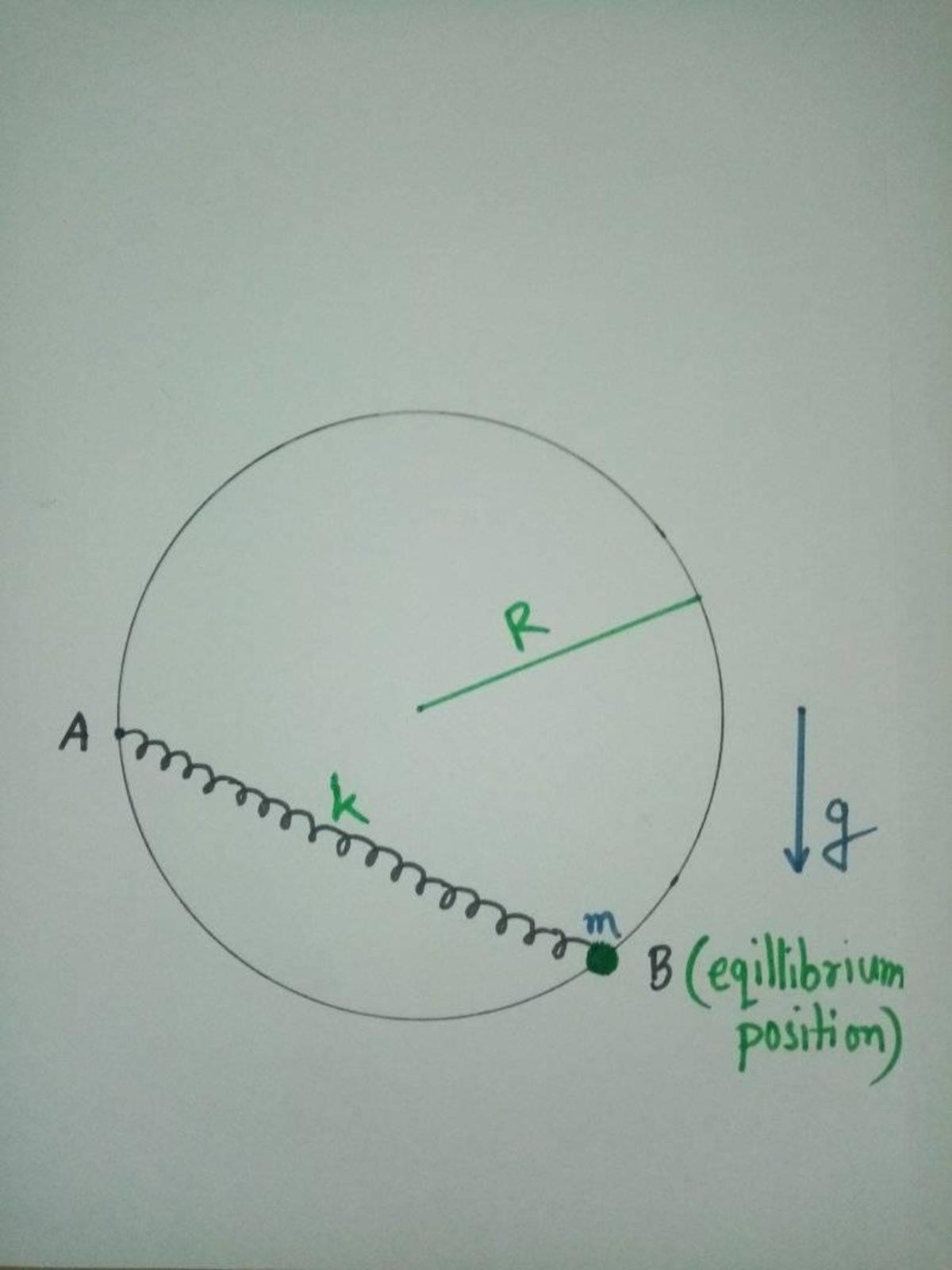 A bead of mass
is attached to a spring of spring constant
. One end of the spring is fixed at the point
shown in the picture. The other end is attached with the bead and the bead can freely move around the rigid circular hoop (frictionless) of radius
. The natural length of the spring is
. When the system is in the shown position, it is found to be in equilibrium.
A bead of mass
is attached to a spring of spring constant
. One end of the spring is fixed at the point
shown in the picture. The other end is attached with the bead and the bead can freely move around the rigid circular hoop (frictionless) of radius
. The natural length of the spring is
. When the system is in the shown position, it is found to be in equilibrium.
Now, if we slightly displace the bead along the hoop, what will be the frequency of the resultant oscillation?
Values and Assumptions:
1) Here , ,
2) Gravitational acceleration
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
This is a very nice problem. At any general time t , let the coordinates of point B be ( R cos ϕ , R sin ϕ ) . The total potential energy of the mass is:
V = V s p r i n g + V g r a v i t y V = 2 K ( 2 R − ( R + R cos ϕ ) 2 + R 2 sin 2 ϕ ) 2 + m g R sin ϕ ⟹ V = sin ϕ + 2 ( 1 − cos ( 2 ϕ ) ) 2
Now, the particle attains equilibrium at that angle where its potential energy is minimum. In other words, the equilibrium configuration satisfies:
d ϕ d V = cos ϕ − sin ϕ + 2 sin ( 2 ϕ ) = 0
Let the equilibrium angle be ϕ e q = α . So: cos α − sin α + 2 sin ( 2 α ) = 0
The above relation will be used later in the solution. Now, since the energy of the system is conserved the sum of its kinetic and potential energy is a constant. This means:
2 ϕ ˙ 2 + sin ϕ + 2 ( 1 − cos ( 2 ϕ ) ) 2 = E
Differentiating the above equation with respect to time and recognising that ϕ ˙ = 0 leads to the equation of motion which is:
ϕ ¨ + cos ϕ − sin ϕ + 2 sin ( 2 ϕ ) = 0
Now, to analyse small oscillations about the equilibrium, we consider the mass to have displaced by a small angle δ from the equilibrium point. In other words, we analyse the system when:
ϕ = α + δ
Where δ is small. Plugging this into the equation of motion and knowing that α is a constant leads to:
δ ¨ + cos ( α + δ ) − sin ( α + δ ) + 2 sin ( 2 α + δ ) = 0
Expanding all the terms using trigonometric identities and applying the small angle approximation sin δ ≈ δ and cos δ ≈ 1 leads to the following. The steps involved here are left out in this solution. The reader may attempt this him/her self.
δ ¨ + cos α − sin α + 2 sin ( 2 α ) + δ ( − cos α − sin α + cos ( 2 α ) ) = 0
Now, recognising that: cos α − sin α + 2 sin ( 2 α ) = 0
Transforms the linearised equation of motion to:
δ ¨ + ( − cos α − sin α + cos ( 2 α ) ) δ = 0
⟹ ω 2 = − cos α − sin α + cos ( 2 α )
The final step is to calculate α . I did this using a computer. I plotted the potential energy as a function of ϕ in the interval − 2 π ≤ ϕ ≤ 2 π . The minimum occurs at ϕ e q = α = − 1 . 3 1 3 6 r a d .
Finally:
ω = − cos α − sin α + cos ( 2 α ) f = 2 π 1 − cos α − sin α + cos ( 2 α )