Crescent Moon
The Crescent Moon below is formed by two circles, both of which are tangent to each other. The point E is the center of the larger circle. If B H = 9 , and A F = G C = 5 , what is the area of the shaded region?
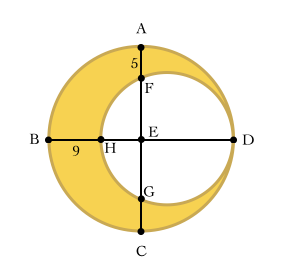
Note : Write your answer to the nearest whole number.
The answer is 643.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Let the radius of the large circle be R . Using Pythagorean theorem , we have:
H F 2 + F D 2 H E 2 + F E 2 + F E 2 + E D 2 ( R − 9 ) 2 + ( R − 5 ) 2 + ( R − 5 ) 2 + R 2 ⟹ R 4 − 3 8 R + 1 3 1 2 R ⟹ R = H D 2 = ( H E + E D ) 2 = ( R − 9 + R ) 2 = R 4 − 3 6 R + 8 1 = 5 0 = 2 5
Let the radius of the small circle be r , then 2 r = H D = H E + E D = 2 R − 9 = 4 1 , ⟹ r = 2 0 . 5 .
The area of the crescent moon A = π ( R 2 − r 2 ) = π ( 2 5 2 − 2 0 . 5 2 ) ≈ 6 4 3
I got 643.5 which i rounded off to 644 and got a response that it is incorrect
Log in to reply
The more accurate answer is 643.2410958, therefore, the nearest integer is 643 not 644.
2 R = 9 + 2 r ⟹ R = 2 9 + 2 r
By the pythagorean theorem , we get
( F E ) 2 = r 2 − ( R − r ) 2 = 2 R r − R 2 ⟹ F E = 2 R r − R 2
However, F E = R − 5
F E = F E
R − 5 = 2 R r − R 2
However, R = 2 9 + 2 r
2 9 + 2 r − 5 = 2 ( 2 9 + 2 r ) ( r ) − ( 2 9 + 2 r ) 2
2 9 + 2 r − 1 0 = 9 r + 2 r 2 − ( 4 8 1 + 3 6 r + 4 r 2 )
2 2 r − 1 = 9 r + 2 r 2 − 4 8 1 − 3 6 r − 4 r 2
Squaring both sides, we get
4 4 r 2 − 4 r + 1 = 9 r + 2 r 2 − 4 8 1 − 3 6 r − 4 r 2
4 4 r 2 − 4 r + 1 = 4 3 6 r + 8 r 2 − 8 1 − 3 6 r − 4 r 2
4 r 2 − 4 r + 1 = 8 r 2 − 8 1 − 4 r 2
− 4 r 2 + 1 = − 8 1
4 r = 8 1 + 1
4 r = 8 2
r = 2 0 . 5
It follows that,
R = 2 9 + 2 ( 2 0 . 5 ) = 2 5
Therefore the area of the shaded region is,
A = π ( R 2 − r 2 ) = π ( 2 5 2 − 2 0 . 5 2 ) ≈ 6 4 3