Criss Cross Loop Flux
A closed loop consists of straight lines from point 1 to point 2 , from point 2 to point 3 , from point 3 to point 4 , and from point 4 to point 1 , as shown in the diagram. The point coordinates are (in x , y , z format):
P 1 = ( 0 , 0 , 0 ) P 2 = ( 1 , 2 , 1 ) P 3 = ( 0 , 1 , 0 ) P 4 = ( 1 , 0 , 0 )
There is a magnetic vector potential all throughout space. The magnetic flux density is the curl of the magnetic vector potential.
A = ( A x , A y , A z ) = ( y , z , x ) B = ∇ × A
Determine the absolute value of the magnetic flux through the loop:
∫ ∫ S B ⋅ d S
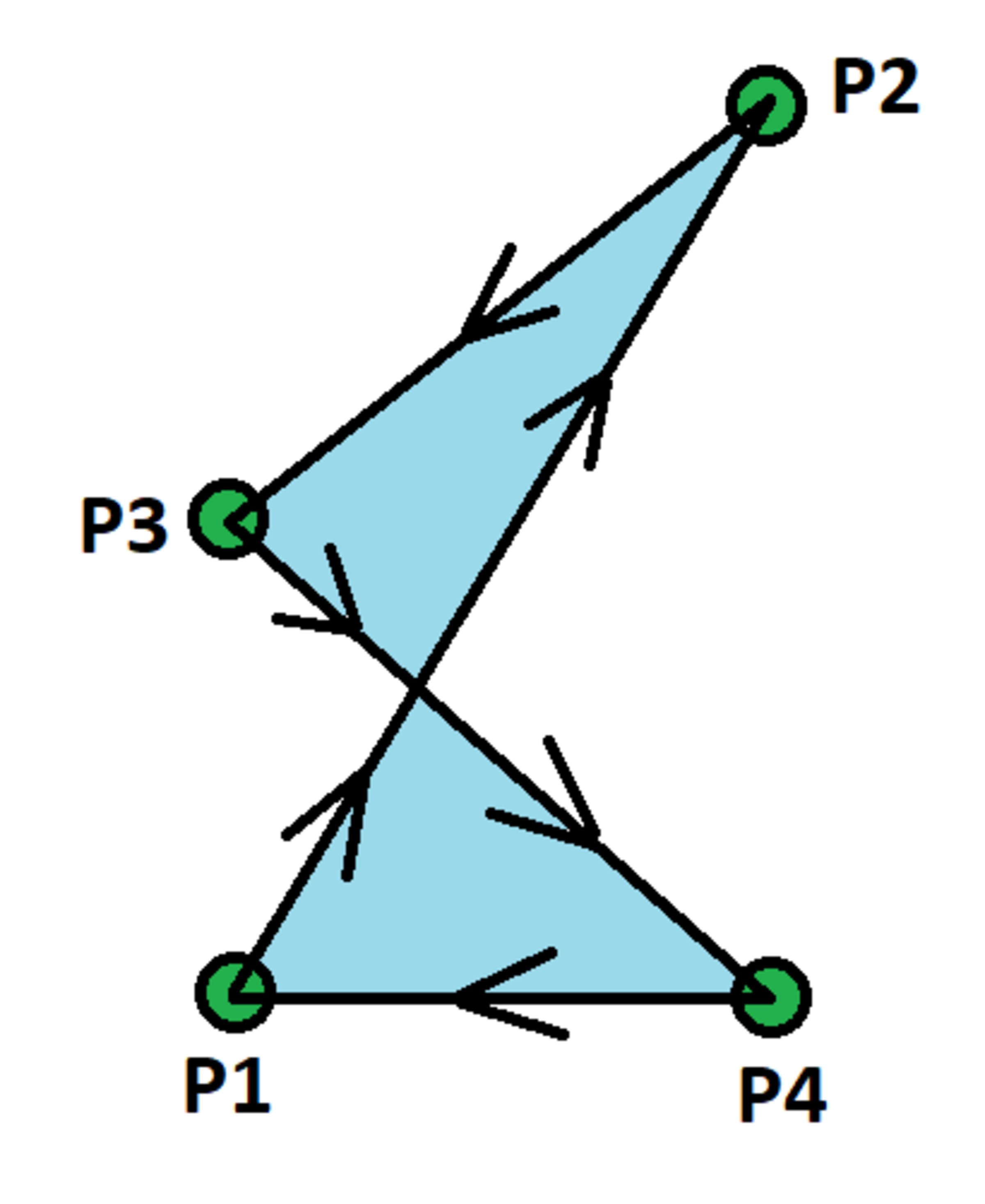
The answer is 0.5.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
@Karan Chatrath
A very nice solution.
By the way I am tired and bored by just calculating Flux Flux Flux.
I have posted a note. Please solve those problem, they are very good and conceptual and tricky problems.
Thanks in advance.
Log in to reply
I will try them when I can. By the way, you recently sent me a problem relevant to flux calculation which you were stuck in. I would recommend that you solve more of such problems instead of expressing your boredom, to strengthen your conceptual understanding. Try solving that previous flux problem that you shared by applying the concept of a magnetic vector potential. It could be a nice alternative method.
The equation of the line connecting P1 and P2 can be parameterised as:
x = t y = 2 t z = t
t varies from 0 to 1 . We have:
A = ( 2 t , t , t ) d r = ( 1 , 2 , 1 ) d t
∫ P 1 → P 2 A ⋅ d r = ∫ 0 1 5 t d t = 2 5
The equation of the line connecting P2 and P3 can be parameterised as:
x = 1 − t y = 2 − t z = 1 − t
t varies from 0 to 1 . We have:
A = ( 2 − t , 1 − t , 1 − t ) d r = ( − 1 , − 1 , − 1 ) d t
∫ P 2 → P 3 A ⋅ d r = − ∫ 0 1 ( 4 − 3 t ) d t = − 2 5
The equation of the line connecting P3 and P4 can be parameterised as:
x = t y = 1 − t z = 0
t varies from 0 to 1 . We have:
A = ( 1 − t , 0 , t ) d r = ( 1 , − 1 , 0 ) d t
∫ P 3 → P 4 A ⋅ d r = ∫ 0 1 ( 1 − t ) d t = 2 1
The equation of the line connecting P3 and P4 can be parameterised as:
x = 1 − t y = 0 z = 0
t varies from 0 to 1 . We have:
A = ( 0 , 0 , 1 − t ) d r = ( 1 , 0 , 0 ) d t
∫ P 4 → P 1 A ⋅ d r = ∫ 0 1 0 d t = 0
Now, the flux through the closed-loop
Φ = ∫ S B ⋅ d S = ∮ C A ⋅ d r
The above identity is found using Stokes' theorem. Then:
Φ = ∮ C A ⋅ d r = ( ∫ P 1 → P 2 A ⋅ d r ) + ( ∫ P 2 → P 3 A ⋅ d r ) + ( ∫ P 3 → P 4 A ⋅ d r ) + ( ∫ P 4 → P 1 A ⋅ d r ) = 2 5 − 2 5 + 2 1 + 0 ⟹ Φ = 2 1