Critical Angle of Precession of a re-assembled top

Classical Mechanics Level 5

Jatin and Anish decided to do an experiment. They bought thousands of right conical tops (of the same base radius and uniform mass densities, but with different heights and semi vertical angles) from a store.

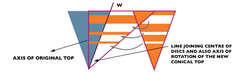
Anish cut the tops parallel to their base into infinite thin discs. Jatin began to reassemble these discs in such a way that the centre of all the discs lie on the slant height of the original top and glued them to make a new rigid structure. They both tried spinning all such tops on the ground about an imaginary axis (straight line joining the centre of the discs or slant height of the original tops) with a constant angular velocity. They observed that a particular top had minimum angular velocity of precession .

The tops precesses in a circle parallel to the base about the axis of the original top with the tip of the top not moving. The semi-vertical angle of this top is $\theta$ . Find $\lfloor \theta \rfloor$

Assume that the new top has a narrow tapered tip.

The answer is 43.

1 solution

Milun Moghe
Mar 7, 2014

Image

Let us consider a ring in xy plane

We have to calculate the moment of inertia of this ring about an axis incnined to the z axis at some angle \theta here it is the semi vertical axis of the cone.

consider a elemental arc of a rind with position vector

$\overrightarrow{r}=R(cos\varphi\hat{i}+sin\varphi\hat{j})$

unit vector along axis of rotation is

$\overrightarrow{a}=(cos\theta\hat{k}+sin\theta\hat{i})$

perpendicular distance from this element

$\left|\overrightarrow{p}\right|^{2}=\left|\overrightarrow{r}\Lambda\hat{a}\right|^{2}=R^{2}\left|\left[\begin{array}{ccc} \hat{i} & \hat{j} & \hat{k}\\ cos\varphi & sin\varphi & 0\\ sin\theta & 0 & cos\theta \end{array}\right]\right|^{2}=R^{2}(cos^{2}\theta+(sin^{2}\varphi*sin^{2}\theta))$

$I=\int dm*p^{2}=\frac{mR^{2}}{2\pi}\int_{0}^{2\pi}(cos^{2}\theta+(sin^{2}\varphi*sin^{2}\theta))d\varphi=\frac{mR^{2}}{2}(1+cos^{2}\theta)$

Then we integrate to form a disc then again integrate to get a cone of moment of inertia

$I_{cone}=\frac{3mR^{2}(1+cos^{2}\theta)}{20}$

The lop is not upright then weight force downwards will provide a torque $\overrightarrow{\tau}$ about the tip which must tend to produce an increase in the angular momentum in the direction of that torque this direction will always be perpendicular to the direction of $\overrightarrow{L}$ hence this torque can never change the magnitude of $\overrightarrow{L}$ but only its direction.

It is seen that L and hence the axis of the new top will precess around in a circle about the vertical line z axis

Let the increase in angular momentum due to the force of gravity produce and angular momentum $d\overrightarrow{L}$ perpendicular to the direction of initial angular momentum

precession angular velocity be $\omega_{p}=\frac{d\varphi}{dt}=\frac{\frac{dL}{Lsin\theta}}{dt}=\frac{\frac{dL}{dt}}{Lsin\theta}=\frac{mgr}{Lsin\theta}=\frac{mgh}{L}=\frac{mgh}{I\omega}$

here r is the distance of centre of mass from the axis of precession and h is the distance of centre of mass from tip of the top. Finally minimizing using derivatives we get $\theta_{min-\omega_{p}}=43.69degrees$

Try also taking any other arrangement other than just lateral shifting the answer will be the same

Milun Moghe - 7 years, 3 months ago

Note that you can edit your own solution, using the edit button to the top right.

You can also let images display directly using markdown code. You can edit your solution to see how I did it. Just type (without spaces)

! [image] (weblink)

Calvin Lin Staff - 7 years, 2 months ago

Critical Angle of Precession of a re-assembled top

The answer is 43.

1 solution

0 pending reports