Critical Angular Velocity of Tilted Rotation

Electricity and Magnetism Level 5

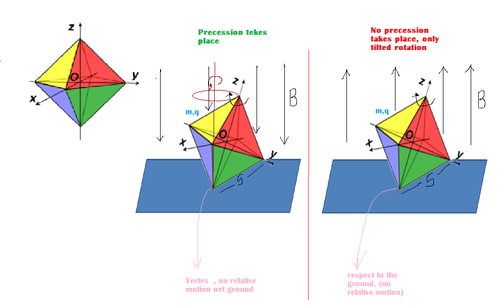A top is rotated in the presence of a uniform magnetic field (directed vertically downwards)on a rough horizontal surface. The top precesses around a vertical axis . Now the polarity of the magnetic field is reversed and again the top is spun with the same angular velocity but now it is observed that top does not precess but undergoes rotation about which ever axis it was rotated initially. Find the angular velocity of the top.

The top in this case is a hollow octahedron of mass $m$ , charge $q$ and side $s$ and the magnetic field has a magnitude $B$ then the critical angular velocity with which the top has to be spun (about an axis passing through two opposite vertices of the octahedron) can be represented as $\omega=a\frac{mg}{qsB}$ then find the units digit of [100a]

Assumptions

The point of contact i.e. vertex is stationary mass and charge is uniformly distributed along the faces.
Refer to gyro -magnetic ratio rather that calculating magnetic moment. For a octahedron ratio of square of radius of gyration to the square is side $s$ is $5/9$ .
$\left[x\right]$ represents the greatest integer function.
In both of the cases the tops are rotating in anti clockwise sense, (not as shown in the figure which is clockwise)

The answer is 4.

1 solution

Milun Moghe
Mar 31, 2014

The torque due to the weight is balanced by torque due to magnetic field about point of contact $mgh(sin\theta)=\mu Bsin\theta$

gyromagnetic ratio gives

$\frac{q}{2m}=\frac{\mu}{L}=\frac{\mu}{I\omega}$ on solving we get $\omega=\frac{9\sqrt{2}}{5}\frac{mg}{qsB}$

You gave wrong direction again. In second case, the torques of both magnetic and gravitational forces are going in the plane. I guess you should have shown $\omega$ anticlockwise(from above).

jatin yadav - 7 years, 2 months ago

Another one I cannot believe this , dont know why this happens with me only??How could I.

Milun Moghe - 7 years, 2 months ago

Why do you ask for units digit of [100 a]. Rather directly ask a. A problem of physics looks good in decimal answer. I did in the same way.

jatin yadav - 7 years, 2 months ago

Sorry about that i just like to make things complicated but some times i mess up with them. I'll try from now onwards to make it simple. Thanks for your advice regarding jee mains.

Milun Moghe - 7 years, 2 months ago

What was the point of the first case involving precession?

Karthik Kannan - 6 years, 11 months ago

Critical Angular Velocity of Tilted Rotation

The answer is 4.

1 solution

0 pending reports