Critical Helical Convergence
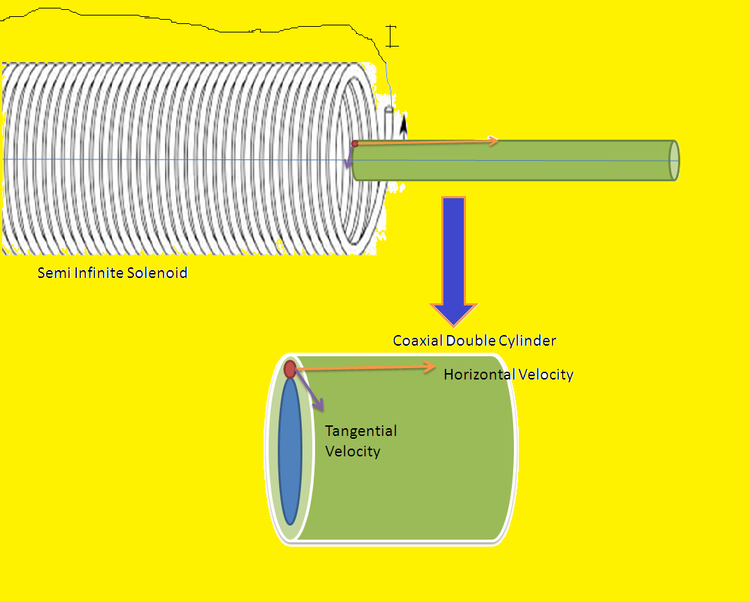 Consider the following setup which consists of a semi-infinite solenoid (in which a constant current
is flowing )connected end to end and coaxially to a double cylindrical set up. The double cylindrical set up consists of two coaxial fixed cylinders of radius r with a very small radii difference. In between the gap of the two cylinders a particle is given a certain horizontal velocity
as well as some tangential velocity
at time t=0. The number of turns density is n. What is the maximum horizontal velocity in
given so that the particle returns to its original position?
Consider the following setup which consists of a semi-infinite solenoid (in which a constant current
is flowing )connected end to end and coaxially to a double cylindrical set up. The double cylindrical set up consists of two coaxial fixed cylinders of radius r with a very small radii difference. In between the gap of the two cylinders a particle is given a certain horizontal velocity
as well as some tangential velocity
at time t=0. The number of turns density is n. What is the maximum horizontal velocity in
given so that the particle returns to its original position?
Details and assumptions:
- The cylinder is also infinitely long
- There is no friction or no collisions between the cylinder and particle.
The answer is 4.019.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The flux through the surface can be related with field by gauss law of magnetism or the maxwells equation. ∮ B ⋅ d S = 0
∫ C D B ⋅ d S = ∫ A B B ⋅ d S + ∫ A B C D B ⋅ d S ABCD represents the curved surface while AB and CD the base let 2 μ o n I = c
c π r 2 = ∫ 0 z 2 π r d z B r + c ( 1 − z 2 + R 2 z ) π r 2 Applying newton's leibnitz differenciation we get B r = 2 c ( R 2 + z 2 ) 2 3 r R 2 As the magnetic force doesn't do any work the speed remains the same V o = V 1 2 + V 2 2 = V 1 0 2 + V 2 0 2 − m d x V 1 d V 1 = B r V 2 q Integrating and applying appropriate limits we get V 2 = V 2 o + 2 m q c r x 2 + R 2 x If the particle has zero horizontal velocity on its path then it will return back in a helical path . for this V 0 = V 2 V 0 = V 2 o + 2 m q c r x 2 + R 2 x V 1 < ( 4 m q r μ o n I ) 2 + V 2 0 ( 4 m q r μ o n I )
If the horizontal velocity exceeds this then the particle will go to infinity and not return.