Crop Circles!

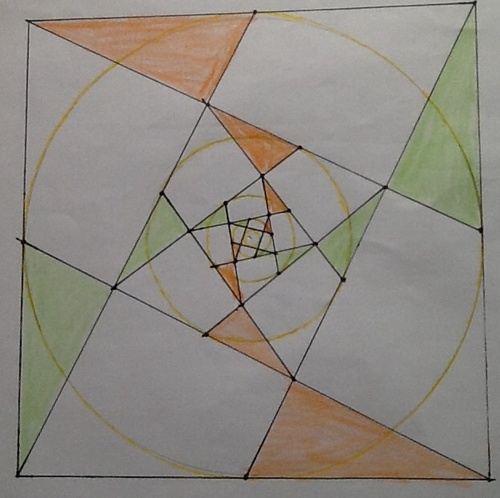Consider the above diagram. This pattern is obtained by joining the vertices of the square with the midpoints of one of the opposite sides of square. These lines create another square, where the same process continues. Now, in each new square created, the largest possible circle which can fit in that square is drawn.

Let $A_n$ be the difference of the area between square created in the $n^{th}$ iteration of the pattern, and the circle inscribed in it. Say this pattern is done on a $1$ hectare plot. Find $A_4$ , rounded to the nearest tenth, in metres squared .