Cross section of a cube and a plane (part 2)

The plane containing the pentagon must intersect 5 cube's faces from which 2 pairs are parallels. The intersection of a plane with 2 parallels plane is 2 parallels lines. So the pentagon has 2 pairs of parallels edges and could not be regular.

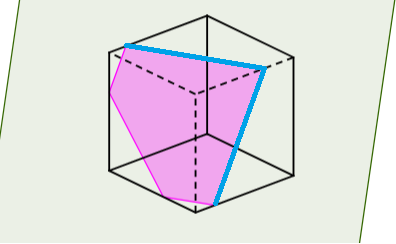
For the plane section to make a pentagon, two of the sides of the cube must be cut as shown in blue. They intersect opposite sides of the square. The angle between these segments must be acute.

A regular pentagon has all angles greater than 90 degrees. Therefore the pentagon cannot be regular.

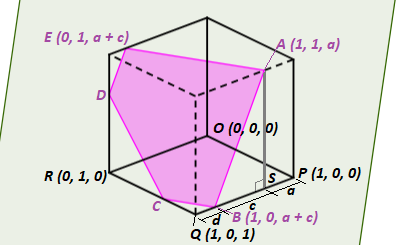
As given by the author's solution, the picture below shows that it is possible for the cross-section to be a pentagon. (Some labels and coordinates were added for the proof below.)

We can show that the pentagon cannot be regular by an indirect proof:

Assume that the cross-sectional pentagon $ABCDE$ is regular. Then $AB = BC = CD = DE = AE$ . Let the cube be a unit cube, and let $A$ be $a$ away from one of the cube's vertices. Then since $AB = AE$ , and $B$ and $E$ must also be the same distance away from some of the other cube's vertices, and let that distance $BP = a + c$ . (Let the distance from $B$ to the other cube's vertex $Q$ be $BQ = d$ . As a unit cube, $a + c + d = 1$ .) Then the coordinates for $A$ , $B$ , and $E$ are $A (1, 1, a)$ , $B (1, 0, a + c)$ , and $E (0, 1, a + c)$ , and vector $AB = (0, -1, c)$ and vector $AC = (-1, 0, c)$ , and the equation of the cross-sectional plane is $cx + cy + z = a + 2c$ .

Since $C$ is the plane $y = 0$ , $z = 1$ , and $cx + cy + z = a + 2c$ , its coordinates are $C (1 - \frac{d}{c}, 0, 1)$ . Since $D$ is the plane $x = 0$ , $z = 1$ , and $cx + cy + z = a + 2c$ , its coordinates are $D (0, 1 - \frac{d}{c}, 1)$ . Then $DR = 1 - \frac{d}{c}$ , $CR = 1 - \frac{d}{c}$ , and as a unit cube, $CQ = \frac{d}{c}$ .

Now, by Pythagorean's Theorem on $\triangle ASB$ , $AB = \sqrt{c^2 + 1}$ , and by Pythagorean's Theorem on $\triangle BQC$ , $BC = \sqrt{d^2 + \frac{d^2}{c^2}} = \frac{d}{c}\sqrt{c^2 + 1}$ . Since $AB = BC$ , $\sqrt{c^2 + 1} = \frac{d}{c}\sqrt{c^2 + 1}$ , which means $\frac{d}{c} = 1$ . But then $CR = 1 - \frac{d}{c} = 0$ and $DR = 1 - \frac{d}{c} = 0$ , and by Pythagorean's Theorem on $\triangle CRD$ , $CD = 0$ , which means $AB = BC = CD = DE = AE = 0$ , so there is no pentagon, which is absurd. Therefore, our assumption that the cross-sectional pentagon $ABCDE$ is regular is false, which means pentagon $ABCDE$ cannot be a regular pentagon.

[Partial Solution] The above figure shows that it is possible to have a pentagon.

I hope to see insightful solution, to show it is not possible to have regular pentagon, from you.