Cross Twice or More
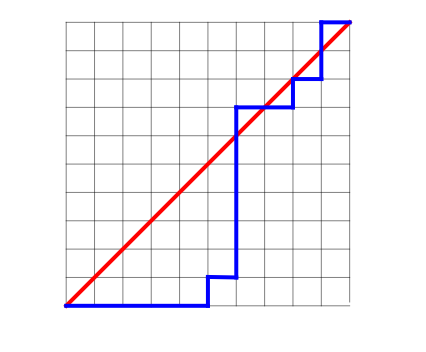 How many ways are there to get from the bottom left corner of a
1
0
×
1
0
grid to the top right corner in 20 steps, if you must cross the main diagonal (in red) two times or more?
How many ways are there to get from the bottom left corner of a
1
0
×
1
0
grid to the top right corner in 20 steps, if you must cross the main diagonal (in red) two times or more?
In the above example, the blue path crosses the red diagonal three times, so it is a valid path.
The paths are monotonic, i.e, only moves to the right and the top are allowed.
The answer is 100776.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
Great problem, and very nicely explained solution! I followed the same method, except for the summation which I calculated by adding the 6 terms manually. I had forgotten this recurrence relation of Catalan numbers.
C n + 1 = i = 0 ∑ n C i C n − i
I was highly motivated to solve this problem cause of your name, haha. Too bad I failed, guess I must read more theory before challenging myself with lv 5 problems.
Really nice problem tho, you got me wondering about the solution for almost an hour.
Log in to reply
Thanks! I'm honored to be a source of motivation for you.
I looked at this, and was confused because I did basically the same thing but without the recurrence and got a different answer. Then I realized that I had changed a plus to a minus in the summation when entering it on a calculator... someday I will learn. ಠ_ಠ
Log in to reply
Yikes, those types of mistakes are the most frustrating.
Log in to reply
AWESOME QUESTION...... AND ALSO NICELY EXPLAINED SOLUTION
Straight-forward path to solution!
That reccurence thing is cool. I just went for
f[n_] := Binomial[2 n, n] -
2 Sum[CatalanNumber[i] CatalanNumber[n - i], {i, 1, n}]
For a general formula, we have ( 2 n n ) − 2 ( C n + 1 − C n ) = ( n + 2 ) ( n − 2 ) ( n − 1 ) C n = ( n + 1 ) ( n + 2 ) ( n − 2 ) ( n − 1 ) ( 2 n n ) .
For n = 1 0 , answer is 1 1 ⋅ 1 2 8 ⋅ 9 ⋅ 1 8 4 ′ 7 5 6 = 1 0 0 ′ 7 7 6 .
It is a bit confusing without top indices
Same way :)
We will proceed with complementary counting: count the number of ways to get to the end with zero or one crossing, and subtract it from the total number of paths possible.
First, the total number is ( 1 0 2 0 ) = 1 8 4 7 5 6 .
Now, let's count the number of paths that do not cross. But we recognize this as a famous problem of "how many paths without going above the diagonal" with the answer simply C 1 0 , where C n is the n th Catalan number. But note that we can either be always below the diagonal or always above it so there are actually 2 C 1 0 ways.
Now, let's count the number of paths that cross exactly once. If the point of crossing is at ( k , k ) , then we have divided the problem into two smaller problems of "how many paths without going above the diagonal". Thus, for this case there are C k ⋅ C 1 0 − k ways. But note that again, we can start out above the diagonal or below the diagonal, so there are 2 C k ⋅ C 1 0 − k ways for each 1 ≤ k ≤ 9 .
Thus, the number of ways for the path to not cross or cross once is 2 C 1 0 + k = 1 ∑ 9 2 C k ⋅ C 1 0 − k = 2 k = 1 ∑ 1 0 C k ⋅ C 1 0 − k
How do we calculate this? We notice that C 1 1 = k = 0 ∑ 1 0 C k ⋅ C 1 0 − k by the recurrence relation of C n so 2 k = 1 ∑ 1 0 C k ⋅ C 1 0 − k = 2 ( C 1 1 − C 0 ⋅ C 1 0 ) = 2 ( 1 2 1 ( 1 1 2 2 ) − 1 1 1 ( 1 0 2 0 ) ) = 8 3 9 8 0
So our final answer is 1 8 4 7 5 6 − 8 3 9 8 0 = 1 0 0 7 7 6