Crossing Paths - Revisited
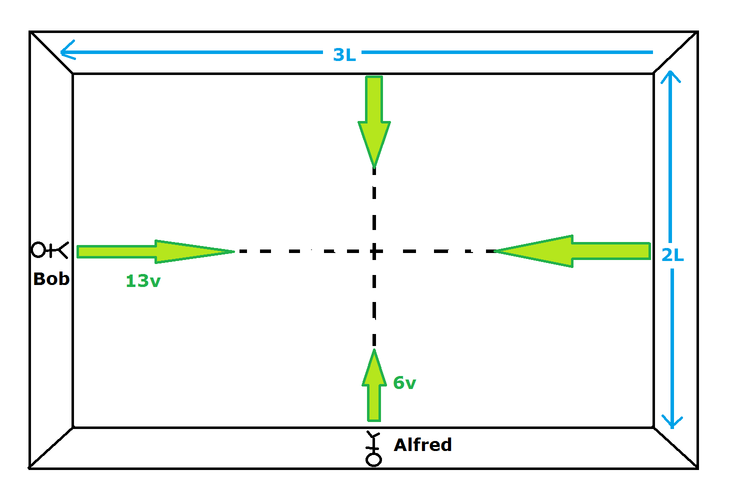 Two astronauts, Alfred and Bob, are at the midpoints of adjacent walls in a rectangular room in a space station. Alfred's wall has length
, and Bob's wall has length
. At the same instant, they both push off their walls and begin floating across the room. Alfred has speed
, and Bob has speed
. As they float, they both get really tired and fall asleep, so that when they reach their opposite walls, they bounce back at the same angle.
Two astronauts, Alfred and Bob, are at the midpoints of adjacent walls in a rectangular room in a space station. Alfred's wall has length
, and Bob's wall has length
. At the same instant, they both push off their walls and begin floating across the room. Alfred has speed
, and Bob has speed
. As they float, they both get really tired and fall asleep, so that when they reach their opposite walls, they bounce back at the same angle.
They keep bouncing forth until they finally collide. The time it takes for them to collide can be expressed as , where and are positive, coprime integers.
Find .
The answer is 5.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Whenever Alfred is at the center of the room, he will have travelled a distance L + 2 n L , where n is some positive integer. Likewise, whenever Bob is at the center, he will have travelled a distance 2 3 L + 3 m L , where m is some other positive integer.
Speed = distance/time, so time = distance/speed. Therefore, Alfred and Bob will be at the center of the room at times:
t A = 6 v L ( 2 n + 1 ) , and t B = 1 3 v 3 L ( m + 2 1 ) .
Setting these times equal to eachother and cancelling out L and v , we get:
6 2 n + 1 = 1 3 3 ( m + 2 1 ) .
Solving this for n we get:
n = 1 3 9 m − 2
The smallest integer pair that satisfies this equation is m = 6 , n = 4 . Plugging n = 4 into Alfred's time equation, we get:
t = 2 v 3 L .
It can be verified that plugging m = 6 into Bob's time equation gives the same result.
The answer, then, is a + b = 5