Crossing the obstacle

Cut the horizontal square and the triangular obstacle into half along diagonal $AC$ . Split open the right triangle into two along its base and flatten it. Then we get the a two-dimensional kite as shown that converts three-dimensional paths into two-dimensional lines.

Then the shortest path is a straight line joining $A$ and $C$ and $AC=1.92 \ \rm m$ . Let the altitude $x=EF$ and $\angle EBF = \theta$ . Then we note that

$\begin{aligned} \sin (\theta + 45^\circ) & = 0.96 = \frac {24}{25} \\ \implies \tan (\theta + 45^\circ) & = \frac {24}{\sqrt{25^2-24^2}} = \frac {24}7 \\ \frac {1+\tan \theta}{1-\tan \theta} & = \frac {24}7 \\ \implies \tan \theta & = \frac {17}{31} \end{aligned}$

Note that $x = BF \cdot \tan \theta = \dfrac {17}{31\sqrt 2}$ . Therefore, $a+b+c = 17+31+2 = \boxed{50}$ .

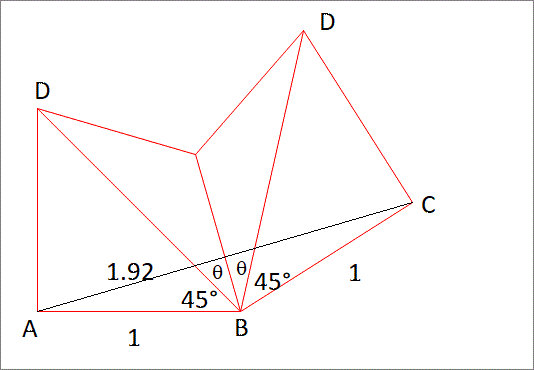
Opening up the four triangles results in the figure above, and one can see immediately that

$\overline{AC} = 1.92 = 2 (1) \sin (45^{\circ} + \theta )$

Hence,

$\sin( 45^{\circ} + \theta ) = 0.96$

From which, $\cos( 45^{\circ} + \theta ) = \sqrt{1 - (0.96)^2 } = 0.28$

Therefore, $\tan( 45^{\circ} + \theta ) = \dfrac{24}{7}$

And it follows that $\tan \theta = \dfrac{ \frac{24}{7} - 1 }{1 + \frac{24}{7} } = \dfrac{17}{31}$

The height $x = \dfrac{\sqrt{2}}{2} \tan \theta = \dfrac{ 17 }{31 \sqrt{2} }$

Hence, the answer is $17 + 31 + 2 = \boxed{50}$

Label the diagram as follows, and let $p = MN$ and $q = BO$ :

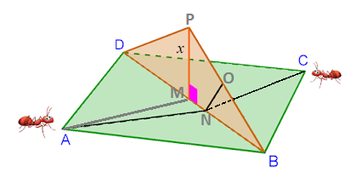
As half the diagonal of square $ABCD$ with unit sides, $AM = MB = \frac{\sqrt{2}}{2}$ , and by the Pythagorean Theorem on $\triangle AMN$ , $AN = \sqrt{p^2 + \frac{1}{2}}$ .

Also by the Pythagorean Theorem on $\triangle MBP$ , $PB = \sqrt{x^2 + \frac{1}{2}}$ .

To minimize the path, $\angle NOB = 90°$ , so $\triangle MBP \sim \triangle OBN$ by AA similarity, so $\frac{NO}{NB} = \frac{MP}{PB}$ , or $\frac{NO}{\frac{\sqrt{2}}{2} - p} = \frac{x}{\sqrt{x^2 + \frac{1}{2}}}$ , so that $NO = \frac{(\frac{\sqrt{2}}{2} - p)x}{\sqrt{x^2 + \frac{1}{2}}}$ .

By symmetry, Brilli Ant's path is $L = 2(AN + NO) = 2(\sqrt{p^2 + \frac{1}{2}} + \frac{(\frac{\sqrt{2}}{2} - p)x}{\sqrt{x^2 + \frac{1}{2}}})$ . Since the function of $L$ is concave up, the minimum occurs when $\frac{dL}{dp} = \frac{2p}{\sqrt{p^2 + \frac{1}{2}}} - \frac{2x}{\sqrt{x^2 + \frac{1}{2}}} = 0$ , which is when $p = x$ and when $L = 2(\sqrt{x^2 + \frac{1}{2}} + \frac{(\frac{\sqrt{2}}{2} - p)x}{\sqrt{x^2 + \frac{1}{2}}}) = \frac{2x + \sqrt{2}}{\sqrt{2x^2 + 1}}$ .

If the shortest path is $192 \text{ cm}$ , then $\frac{2x + \sqrt{2}}{\sqrt{2x^2 + 1}} = 1.92$ , which solves to $x = \frac{17}{31\sqrt{2}}$ for $x < \frac{\sqrt{2}}{2}$ . Therefore, $a = 17$ , $b = 31$ , $c = 2$ , and $a + b + c = \boxed{50}$ .

If we flatten down the obstacle on the plane of the square, we notice that the altitude $EF$ of the isosceles triangle $\triangle EBD$ lies on the diagonal $AC$ .
$AF=FC=\frac{\sqrt{2}}{2}$ and in the case $x>\frac{\sqrt{2}}{2}$ (figure 1), the shortest path from $A$ to $C$ would be $A\to B\to C$ , but this is 2 meters long. Hence, $x\le \frac{\sqrt{2}}{2}$ as in figure 2. Consequently, on his way from $A$ to $C$ , ant-Brilly has to reach some point either of side $EB$ , or side $ED$ . Due to symmetry, we can search for the closest point from $A$ to $EB$ . This, obviously, is the foot of the perpendicular from $A$ to $EB$ . Let’s call it $K$ and denote its length in meters by $d$ . Since the shortest path from $A$ to $C$ is $192cm$ we have $d=0.96$ . Then, for the acute angle $\angle BAK=\theta$ , in $\triangle ABK$ we have $\cos \theta =\dfrac{AK}{AB}=\dfrac{d}{1}=0.96 \ \ \ \ \ (1)$

Moreover, in $\triangle AEK$ , $\begin{aligned} \cos \left( \angle EAK \right)=\frac{AK}{AE} & \Rightarrow \cos \left( \frac{\pi }{4}-\theta \right)=\frac{d}{\frac{\sqrt{2}}{2}+x} \\ & \Rightarrow \left( \frac{\sqrt{2}}{2}+x \right)\left( \cos \theta \cdot \cos \frac{\pi }{4}+\sin \theta \cdot \sin \frac{\pi }{4} \right)=d \\ & \Rightarrow \left( \frac{\sqrt{2}}{2}+x \right)\frac{\sqrt{2}}{2}\left( \cos \theta +\sin \theta \right)=d \\ & \overset{\left( 1 \right)}{\mathop{\Rightarrow }}\,\left( \frac{1}{2}+\frac{x}{\sqrt{2}} \right)\left( d+\sqrt{1-{{d}^{2}}} \right)=d \\ & \Rightarrow \left( \frac{1}{2}+\frac{x}{\sqrt{2}} \right)\left( 0.96+\sqrt{1-{{\left( 0.96 \right)}^{2}}} \right)=0.96 \\ \end{aligned}$

which solves to $x=\frac{17}{31\sqrt{2}}$ Thus, $a=17$ , $b=31$ , $c=2$ and the answer is $a+b+c=\boxed{50}$ .