Crux In Magnetic Flux(part 2)

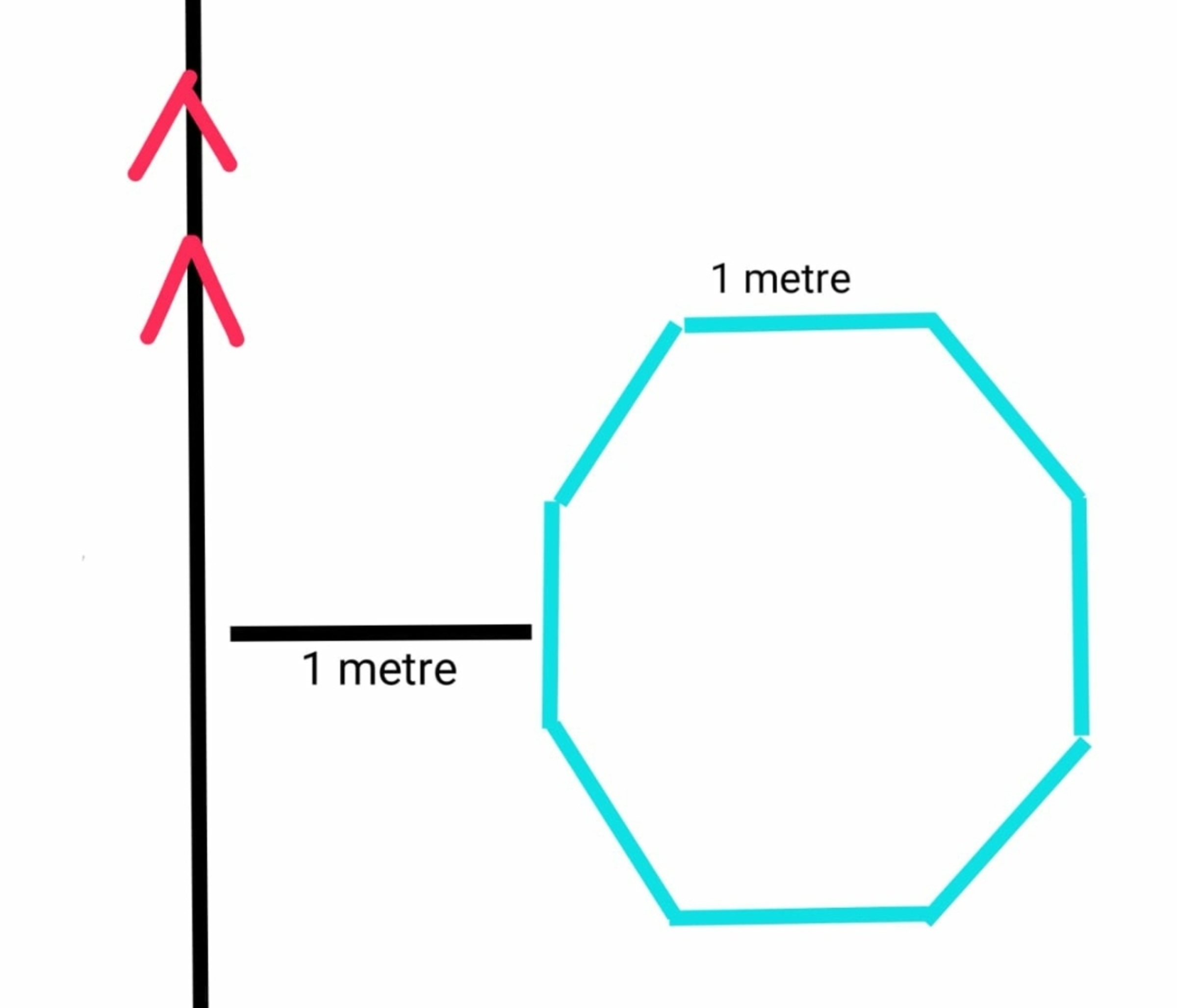
Electricity and Magnetism Level pending

A infinitely long wire carry a current of I I A A . A regular Octagon of side length 1 1 m m placed in the same plane of wire at a perpendicular distance of wire at a perpendicular distance of 1 1 m m from its nearest side to the wire. Calculate the total flux passing through the Octagon. If your answer comes in the form a μ 0 I 2 π \frac{a\mu_{0}I}{2π} ​

Find a upto two decimal places. If your answer comes in the form 1.98731 . Type it as1.98


The answer is 2.39.

A Former Brilliant Member by A Former Brilliant Member

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

Steven Chase
Feb 22, 2020

This is a nice magnetic flux exercise. It can be solved by splitting up the octagon into three regions (left, right, middle) and summing the fluxes for the three regions. Simulation code is attached, with results printed at the end. 

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
 
import math

u0 = 1.0
I = 1.0

mult = u0*I/(2.0*math.pi)

x1 = 1.0/math.sqrt(2.0)

dx = 10.0**(-6.0)

phi = 0.0

#################################

# Left

x = 0.0   # Here, x is the rightward distance from the left edge of the octagon 

while x <= x1:

    D = 1.0 + x
    B = mult/D

    L = 1.0 + 2.0*x   # L is the vertical height of a strip of area

    dA = L*dx
    dphi = B*dA

    phi = phi + dphi

    x = x + dx

print phi

#################################

# Right

x = 0.0

while x <= x1:   # Here, x is the leftward distance from the right edge of the octagon 

    D = 2.0 + 2.0*x1 - x
    B = mult/D

    L = 1.0 + 2.0*x   # L is the vertical height of a strip of area

    dA = L*dx
    dphi = B*dA

    phi = phi + dphi

    x = x + dx

print phi

#################################

# Middle

x = 0.0

while x <= 1.0:   # Here, x is the rightward distance from the left of the middle portion 

    D = 1.0 + x1 + x
    B = mult/D

    L = 1.0 + 2.0*x1   # L is the vertical height of a strip of area

    dA = L*dx
    dphi = B*dA

    phi = phi + dphi

    x = x + dx

print phi

#################################

print ""
print dx
print (phi/mult)

#0.139963032281
#0.204023493344
#0.38118633437

#1e-06
#2.39506437541

1 Helpful 1 Interesting 1 Brilliant 0 Confused

@Steven Chase Sir can we generalise the result for n sided polygon.

A Former Brilliant Member - 1 year, 3 months ago

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...