Crystal Clear

Geometry Level 2

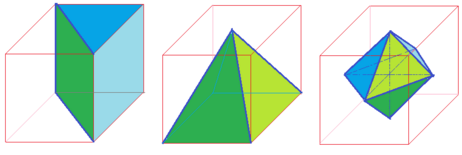
The jewelry shop sells its products cut from the same cubic block in 3 different shapes: a triangular-based prism, a square-based pyramid, and an octahedron. The prism has the base area equal to half the area of the cube's base while the octahedron has its 6 vertices on the centers of the cube's faces, and all 3 shapes have the same height as shown in the picture.

Which of these choices would give you more crystal?

I. A full triangular prism or
II. A pyramid plus an octahedron

Option I Option II Doesn't matter. Both options have got the same amount. Not enough information

View wiki
Worranat Pakornrat by Worranat Pakornrat , 36, Thailand

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

Let V V be the volume of the original cube. Then it's obvious that the prism's volume = V 2 \dfrac{V}{2} because its base is half of the square.

Then the pyramid's volume = V 3 \dfrac{V}{3} for typical pyramid's formula.

Finally, for the octahedron, when we cut this shape in half, we will obtain 2 identical square-based pyramids, and each pyramid has half of the cube's height and half of the cube's base, for its diagonal equals to the cube's side length S S . Hence, base area = ( 1 2 ) ( S 2 ) (\frac{1}{2})(S^2) = half of the original square.

As a result, the volume of the octahedron = 2 × ( 1 2 ) × ( 1 2 ) × ( V 3 ) 2\times(\dfrac{1}{2})\times(\dfrac{1}{2})\times(\dfrac{V}{3}) = V 6 \dfrac{V}{6} .

Therefore, V 2 \dfrac{V}{2} = V 3 \dfrac{V}{3} + V 6 \dfrac{V}{6} , or both options have got the same amount of crystals.

3 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...