Cube and Octahedron Intersection

Geometry Level pending

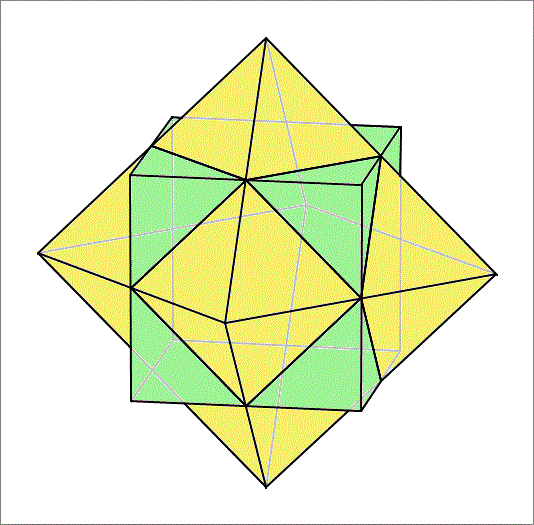
The figure above shows a cube and an octahedron having the same center intersecting. The solid formed by their intersection is shown below. The intersection is the region that is inside the cube and inside the octahedron. Its faces are squares and equilateral triangles with the same side length. If that side length is equal to 1 1 , then find the volume of the solid.


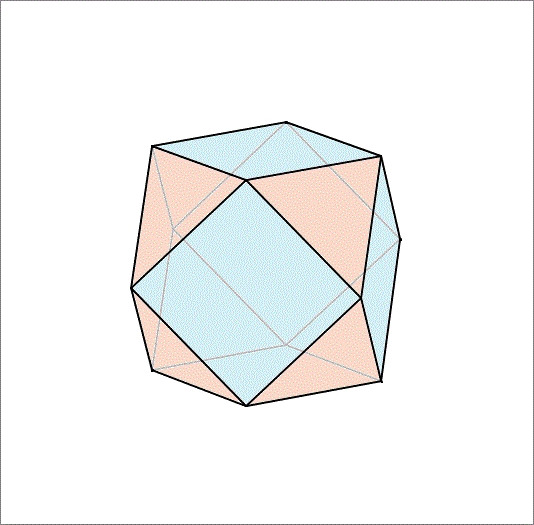
The answer is 2.357.

Hosam Hajjir by Hosam Hajjir , 56, Canada

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

Hongqi Wang
Dec 12, 2020

V = V c u b e − 8 ⋅ V c o n e = ( 2 ⋅ 2 2 ) 3 − 8 ⋅ 1 3 ⋅ [ 1 2 ( 2 2 ) 2 ] ⋅ 2 2 = 2 2 − 1 3 2 = 5 3 2 \begin{aligned} V &= V_{cube} - 8 \cdot V_{cone} \\ &= \left (2 \cdot \dfrac {\sqrt 2}{2} \right )^3 - 8 \cdot \dfrac 13 \cdot \left [\dfrac 12 \left (\dfrac {\sqrt 2}2 \right )^2 \right ] \cdot \dfrac {\sqrt 2}2 \\ &= 2 \sqrt 2 - \dfrac 13 \sqrt 2 \\ &= \dfrac 53 \sqrt 2 \end{aligned}

1 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...