Cube Art Choices

A brief introduction to the approach I am using:

• The approach I have learned for this type of problem is detailed very nicely in the textbook Groups and Symmetry by M. A. Armstrong. See Chapter 18 for examples. I wasn't sure how much abstract algebra was on this site (and I've been gone for a long while), so I'm a bit curious if there are other (perhaps more painless) ways to solve this.

• I will be using abstract algebra terminology. If you are not familiar with it, I encourage you to look into the subject if you are feeling adventurous! :)

First off, we recognize the group $G$ of rotational isometries of a cube. The cube can be rotated in several ways such that it fills the same space as before, but some points on the cube have been moved around. Here are the possibilities, where I have labeled the unique rotations as $r$ , $r^2$ , $s$ , and $t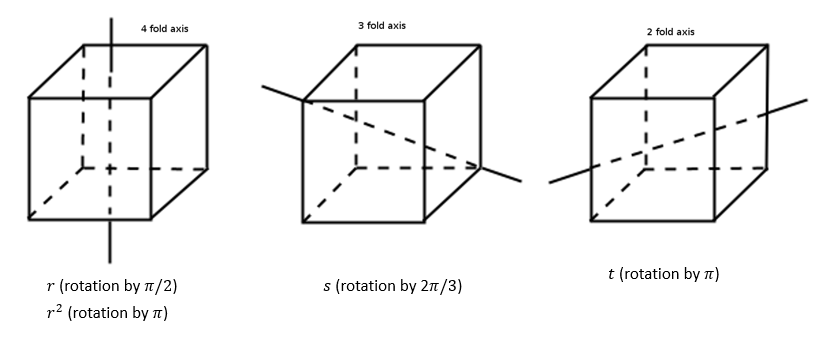$ : (image credit: here )

There are 24 squares total, so we have a set $C$ of $n^{24}$ colorings total (not just different colorings). We consider the action of $G$ on $C$ . Let the set $C_g$ be the subset of $C$ of colorings which are fixed by the action of $g \in G$ .

I will be using the following results. Proofs for the first two are provided in Chapter 18 of the textbook mentioned at the top of this post:

• The Polya Enumeration Theorem: The number of distinct orbits of the action of $G$ on $C$ is equal to $\frac{1}{|G|} \sum_{g \in G} |C_g|$

• The elements of $G$ which are conjugate fix the same number of points in $C$ .

• The sizes of the conjugacy classes (which partition $G$ since conjugacy is an equivalence relation) containing $r$ , $r^2$ , $s$ , and $t$ are 6, 3, 8, and 6, respectively. This can be worked out manually.

• It is easily proven that $G \cong S_4$ , so $|G| = 24$ since $|S_4| = 4! = 24$ .

So, we now work to find all orbits created by rotations $r$ , $r^2$ , $s$ , $t$ and $e$ (the identity). To do this, we first find the sizes of $C_g$ for these elements:

• $r$ : When the cube rotates by $r$ , the squares on the vertical faces are moved in orbits of size 4, since clearly applying $r$ 4 times gives the identity of $G$ . In addition, there is one orbit of size 4 for each of the top and bottom faces. Since all squares in each orbit must be colored the same color, we have $n$ choices of colors for each orbit. This gives us $|C_r| = n^{4 + 1 + 1} = n^6$ .

• $r^2$ : We find that there the vertical faces have 8 orbits of size 2, whereas there are 2 orbits of size 2 on each of the top and bottom faces. This gives us $|C_{r^2}| = n^{8 + 2 + 2} = n^{12}$ .

• $s$ : A bit trickier to visualize, but we find that there are 2 orbits of size 3 on the faces, which leads to a total of 8 orbits of size 3 on the squares since there are 4 squares per face. So, we have $|C_s| = n^8$ .

• $t$ : We find that this rotation creates 12 orbits of size 2 (3 orbits of size 2 on the faces), so $|C_t| = n^{12}$ .

• $e$ : Don't forget this guy! The identity element of $G$ by definition fixes every square, so $|C_e| = n^{24}$ . Keep in mind that though it might sounds silly to consider this a rotation (doing nothing), this isometry is necessary for $G$ to be a group.

We can now apply the Polya Enumeration Theorem, but we would have to do this for every element of $G$ . This is where the second result comes in: Since every element conjugate to $g$ fixes the same number of points as $g$ , multiplying $|C_g|$ by the size of the conjugacy class containing $g$ gives the number of orbits created by the elements in the conjugacy class of $g$ . Thus, applying the Polya Enumeration Theorem along with the third and fourth results now gives us: $\begin{aligned} k & = \frac{1}{24}(6 \times n^6 + 3 \times n^{12} + 8 \times n^8 + 6 \times n^{12} + 1 \times n^{24}) \\ & = \frac{1}{24}n^{24} + \frac{3}{8}n^{12} + \frac{1}{3}n^8 + \frac{1}{4}n^6 \end{aligned}$ So our final solution is $1 + 24 + 3 + 8 + 1 + 3 + 1 + 4 = \boxed{45}$ .