Cube Calendar
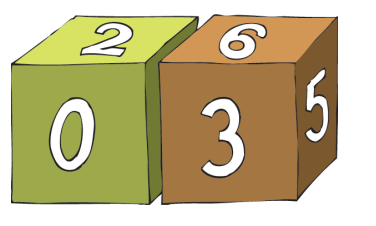
Peter uses two cubes to show the days of the months. On each face of a cube, there is a digit displayed. For example, in the image above, he is showing day 03 of the month.
The cubes can be rotated, and have their positions swapped. Furthermore, the face with a value of 6 can be flipped upside-down to obtain the value of 9. This allows us to display all 31 days of the month.
In the image above, what is the sum of the numbers on the 4 hidden faces of the green cube?
Problem from OBMEP 2011.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Note that the number 0 need to appear in both cubes intent to make the dates from day 01 to 09. Note that the numbers 1 and 2 need to be in both cubes too, intent to make the dates of day 11 and day 22.
Thus we have at this point:
In the table above the numbers in bold is the number that need to be and not appear in the brown cube.
The numbers with * is the numbers left to be in the cubes, not appear in the visible faces and need to be in green cube because of the number of faces left.
The number with **, is the number that not appear in the green cube and need to be in it.
The "normal" numbers is the numbers visible in the image.
Thus the only numbers that not appear in the green cube is 1, 4, 7 and 8, and they sum is 2 0 .