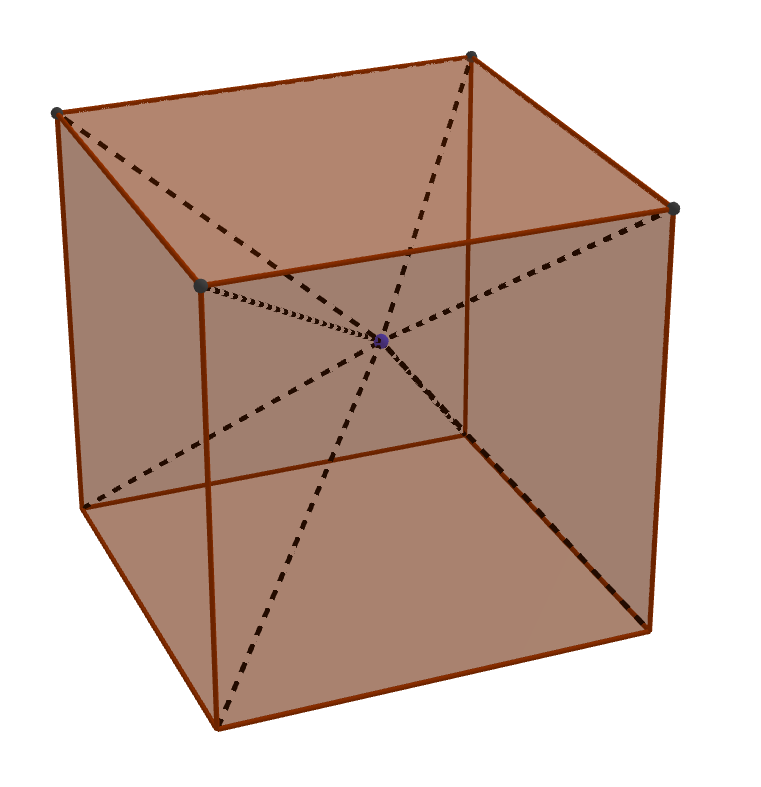
Cube decomposition
Geometry
Level
2
A point is picked inside a cube so that it is decomposed into 6 pyramids, the bases being the faces of the cube. The volumes of five of those pyramids are 2, 5, 10, 11, and 14.
What is the volume of the sixth pyramid?
1
4
6
9
12
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
The volume of any of the pyramids is V = 3 a 2 . h where a is the side length of the cube and h the height of the pyramid.
Hence the volume of two pyramids that face each other (sharing only their apex) is V = 3 a 2 . h 1 + 3 a 2 . h 2 = 3 a 2 . ( h 1 + h 2 ) = 3 a 3 meaning we can organize the 6 volumes of the pyramids to form 3 couples of numbers with the same sum ( 3 a 3 ) .
The only solution is ( 1 4 , 2 ) , ( 1 1 , 5 ) and ( 1 0 , x ) ⇒ x = 6 .