Cube in a spherical octant
A cube is inscribed and bounded by a hollow sphere of radius and the coordinate planes in the first octant where . One edge of the cube lies completely in the horizontal plane, while four vertices lie on the curved surface of the sphere. In addition, one vertex lies on the plane and one vertex lies on the plane. Find the side length of this cube. If the side length is , then enter .
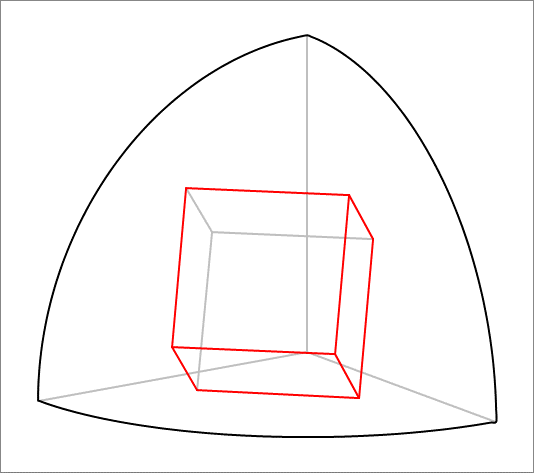
The answer is 5011.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
First we need to relocate our perspective to the one where this "one edge of the cube lies completely in the horizontal xy plane" becomes just a point, specifically, one where this particular edge becomes a vertex of the cube's 2-D square rendering on a plane halfway between xz- and yz- planes (45° from both and through the z-axis, bisecting?).
From the new POV, our square with sides 2m is touching the xy plane base on one vertex (actually the above-mentioned edge, but we're truly only taking its midpoint here). The other two cube vertices lying on xy and xz are now combined as their midpoint as another vertex of this square, kind of leaning towards but is m distance away from z-axis (perpendicularly) because as I already said, this is the midpoint of an edge and not the cube's vertices touching two different planes (bird's eye view sketches can help a lot here).
If the diagram is all set up, it makes sense to imagine that the lines from origin O to the two other square's vertices that haven't been mentioned before to be equal in length since all four of the cube's vertices touched the spherical surface with the same radius of 1. Similarly, the nearest two earlier vertices also must have the same distance from origin O, let's note this distance as x.
The nearest midpoint from z-axis must have a height of √(x² – m²) from the xy plane base. Therefore,
(square's side)²
= (inclined horizontal distance)² + (inclined vertical distance)²
(2m)² = (x – m)² + (√(x² – m²))²
4m² = 2x² – 2xm
2m² = x² – xm
(x – m/2)² = 9m²/4
x = (m ± 3m) / 2 > 0
x = 2m
From here on it's easy to get the answer.
1² = (2m sin 30°)² + (x + 2m cos 60°)² + (2m ÷ 2)²
= m² + [m(2 + √3)]² + m²
= m² × (9 + 4√3)
m = 1 / √(9 + 4√3)
Answer
= floor[10⁴ s]
= floor[10⁴ × 2m]
= floor[20000 / √(9 + 4√3)]
= floor[5011.25614]
= 5011