Cube of Resistors
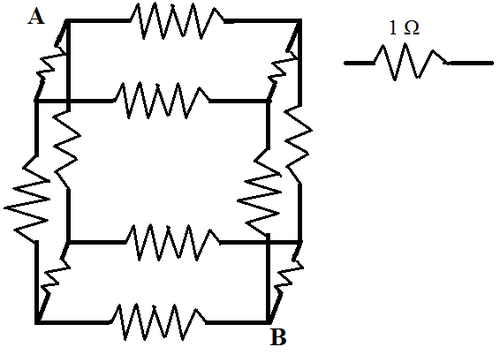Twelve resistors of resistance 1Ω are arranged in such a way that they form a cube, as shown in the image. Find the resistance between points A and B on the cube.
Just to make it more clear, all the resistors are of the same value
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
By symmetry, the three vertices adjacent to A are equipotentials, and so can be coalesced. Similarly, the thee vertices adjacent to B are equipotentials, and so can be coalesced.
The resulting circuit consists of a series of three 1 Ω resistors in parallel, followed by six 1 Ω resistors in parallel, followed by three 1 Ω resistors in parallel, giving a total effective resistance of 3 1 + 6 1 + 3 1 = 6 5 Ω .