Cube roots fun
The real number x satisfies 3 x + 9 − 3 x − 9 = 3 . Find the value of x 2 .
The answer is 80.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
7 solutions
If a-b-c=0 then a^3 -b^3-c^3= 3abc
Used the same method. With graphing calculator also I got 79.99999982. F o r x : x = ± 4 5 .
Let { x + 9 = ( a + b ) 3 = a 3 + 3 a 2 b + 3 a b 2 + b 3 x − 9 = ( a − b ) 3 = a 3 − 3 a 2 b + 3 a b 2 − b 3 . . . ( 1 ) . . . ( 2 )
⇒ 3 x + 9 − 3 x − 9 = 3 ( a + b ) 3 − 3 ( a − b ) 3 = ( a + b ) − ( a − b ) = 2 b = 3 ⇒ b = 2 3
Eq. 1 - Eq. 2: 6 a 2 b + 2 b 3 = 1 8 ⇒ 9 a 2 + 4 2 7 = 1 8 ⇒ a = ± 2 5
From Eq. 1:
x + 9 = ( a + b ) 3 = ( 2 ± 5 + 3 ) 3 = 8 ± 5 5 + 4 5 ± 2 7 5 + 2 7 = 8 ± 3 2 5 + 7 2 = ± 4 5 + 9
⇒ x = ± 4 5 ⇒ x 2 = 8 0
My answer could be a little longer than the others, but I consider it's still functional:
Let's call 3 x + 9 = a and 3 x − 9 = b .
So, the equation can be rewritten: a − b = 3 .
Considering the fact that we're dealing with cubic roots, I used the factorization ( a − b ) ( a 2 + a b + b 2 ) = a 3 − b 3 .
For the sake of simplicity and clarity, I'll define F = a 2 + a b + b 2 .
Multiplying both sides of equation by F, we obtain: a 3 − b 3 = 3 F .
The LHS can be simplified as follows: a 3 − b 3 = ( x + 9 ) − ( x − 9 ) = 1 8 .
Then, the equation reduces to: F = 6 .
We can stablish the non-linear two-equation system: { a − b = 3 a 2 + a b + b 2 = 6
There are many ways to solve it. The way I implemented was to rewrite conveniently the second equation, so it's possible substitute the first one into it:
a 2 − 2 a b + b 2 + 3 a b = 6
( a − b ) 2 + 3 a b = 6
3 a b = − 3 ⇒ a b = − 1
Writing back the expressions of a and b, and multiplying the roots, we obtain:
3 x 2 − 8 1 = − 1 ⇒ x 2 − 8 1 = − 1 ⇒ x 2 = 8 0
Hope you enjoy this answer!
NOTE: This is my first contribution to this great community. Please, don't be so rude! :)
Great solution, up voted.
Our solution will require very little computation.
Recall the cubic formula: The solutions of t 3 + 3 q t − 2 r = 0 are t = 3 q 3 + r 2 + r − 3 q 3 + r 2 − r , which is the "format" of the LHS of the given equation, with r = 9 and x = 3 q 3 + r 2 .
Our idea is to find the cubic f ( t ) = t 3 + 3 q t − 1 8 with f ( 3 ) = 0 . We see that q = − 1 , and f ( t ) = t 3 − 3 t − 1 8 . Now the cubic equation gives 3 8 0 + 9 − 3 8 0 − 9 = 3 , so that x = 8 0 and x 2 = 8 0 .
Moderator note:
Very rare to see a cubic formula implemented. Great job!
Damn nicely done
WE SIMPLY whole cube both side getting 27 on the RHS..then (x+9)-(x-9)-3.cuberoot(x square - 81).(3)....as "a-b=3" see carefully..so 18 -{9.cube root (x square -81)} = 27...on simplifying -1=cube root(x square -81)......-1=x^2 - 81..........x^2=80...is ur ans
we can rewrite this equation as (x+ 9)^ 1/3 = 3 + (x-9)^ 1/3 now we cube both sides , getting X+9 = 27+x -9 +3.3 (( x -9) ^ 1/3) ( 3 + ( x-9 ) ^ 1/3)) we can substitute the left side of the 1st equation and cancel Which are needed to get 9+9 ( x ^2-81)^ 1/3 =0 cancelling 9 we get (x^2-81)^ 1/3 = -1. now we can cube and solve for x^2 to get x^2 = 80
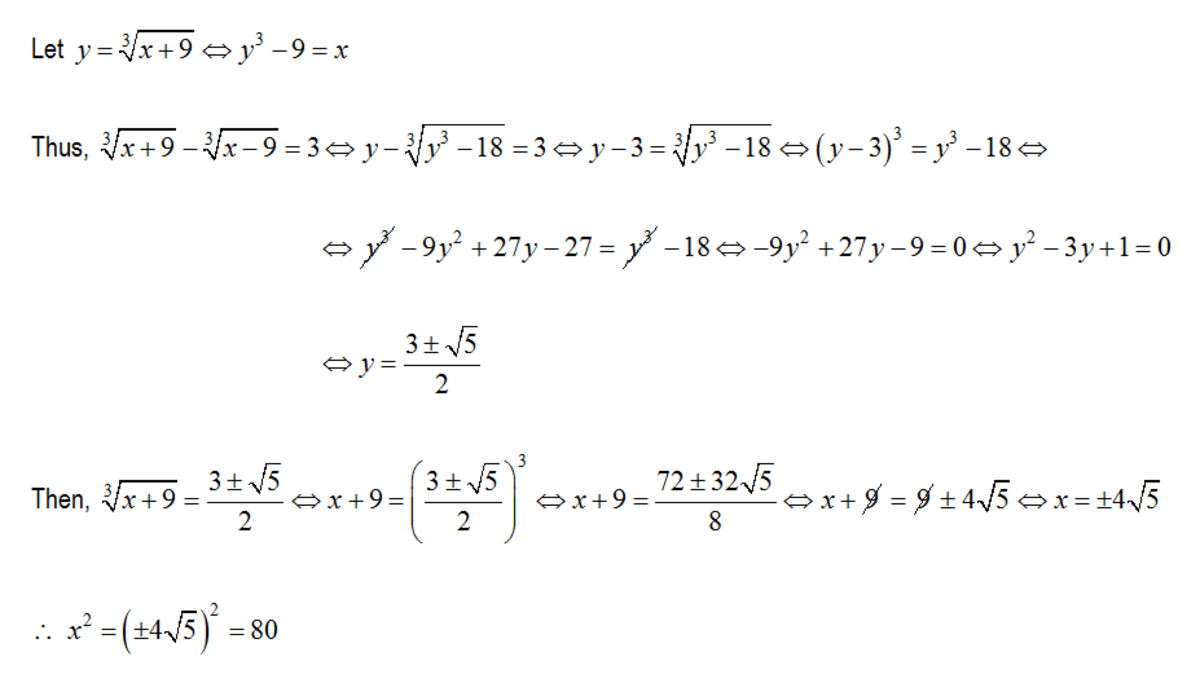
Cube both sides and factor to get: 1 8 − 3 3 ( x + 9 ) ( x − 9 ) ( 3 x + 9 − 3 x − 9 ) = 2 7 .
Simplifying and substituting 3 for 3 x + 9 − 3 x − 9 , we get: − 3 x 2 − 8 1 = 1 .
From here, we simply cube both sides and add 81 to get x 2 = 8 0 .