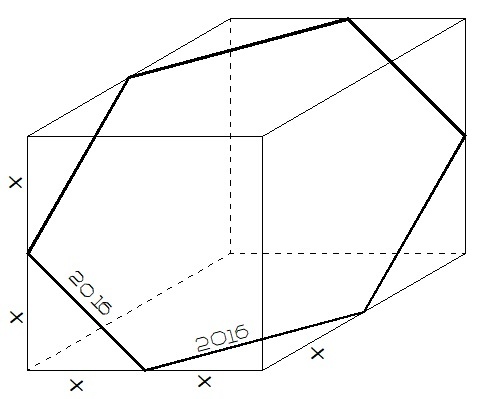
Cube Sliced In Half

The cube was divided equally by a regular hexagon as shown. The vertices of the hexagon lie at the midpoints of the edges. The surface area of the given solid is equal to half the surface area of the cube plus the area of the regular hexagon. By pythagorean theorem, we have

$2016^2=2x^2$ or $x^2=2032128$

So,

$A=\dfrac{1}{2}(6)(2x)^2+\dfrac{3}{2}\sqrt{3}(2016)^2=12(2032128)+6096384\sqrt{3}\approx \boxed{34944783}$

Note:

1. $\text{surface area of a cube} =6a^2$ where $a$ is the edge length of the cube.

2. $\text{area of a regular hexagon} = \dfrac{3}{2}\sqrt{3}a^2$ where $a$ is the edge length of the hexagon.

Assuming the two halves are symmetric, each cut edge is of length 2016, and so the new surface is a regular hexagon.

The total area is half the surface area of the cube plus the area of the hexagon of side 2016. Each 2016-long edge forms the base of an isosceles right triangle with the other two sides being half of a side of the cube. So half the side length is $2016/\sqrt{2}$ , and the side length is thus $2016\sqrt{2}$ . The total area is therefore:

$(6 \times (2016\sqrt{2})^2)/2 + 3\sqrt{3}/2 \times 2016^2 = 34944782.83$

By pythagorean theorem, we have

$2016^2=x^2+x^2$

$x^2=2032128$

$x=\sqrt{2032128}$

$2x=2\sqrt{2032128}$

The area of a regular hexagon is given by $A_H=\dfrac{3}{2}\sqrt{3}a^2$ where $a$ is the side length. So the area of the hexagon is

$A_H=\dfrac{3}{2}\sqrt{3}(2016^2)=6096384\sqrt{3}$

The desired surface area is half of the surface area of the cube plus area of the hexagon, we have

$A=\dfrac{6(2x)^2}{2}+A_H=\dfrac{6(2\sqrt{2032128})^2}{2}+6096384\sqrt{3}\approx$ $\boxed{34944783}$