Cube to cuboid
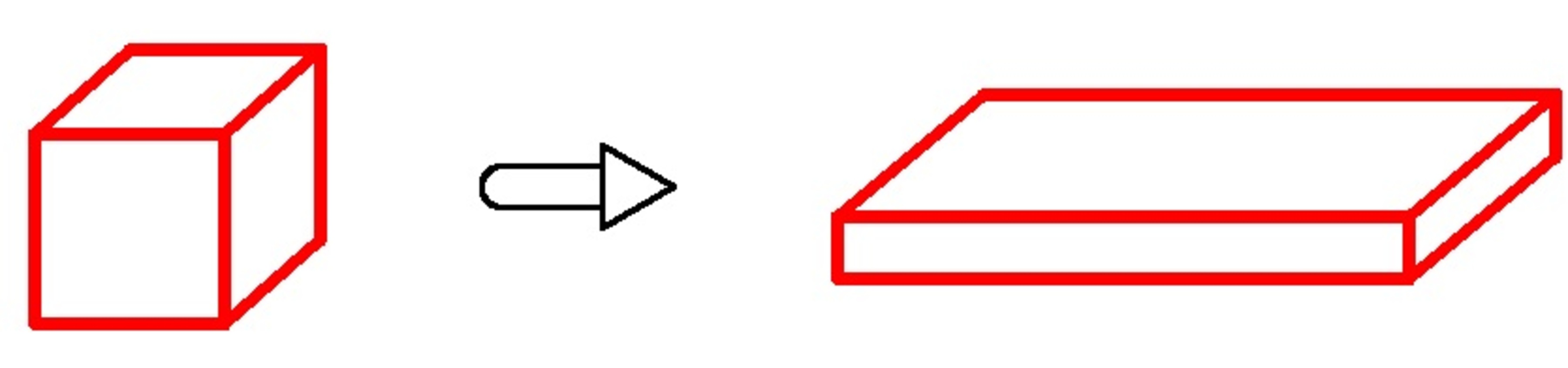 The golden cube (left photo) has a side length of
. It is to be melted to form a golden cuboid (right photo) with a base dimension of
. What is the ratio of the surface area of the cube to the surface of the cuboid? If your answer is of the form
, where
and
are coprime positive integers, find
.
The golden cube (left photo) has a side length of
. It is to be melted to form a golden cuboid (right photo) with a base dimension of
. What is the ratio of the surface area of the cube to the surface of the cuboid? If your answer is of the form
, where
and
are coprime positive integers, find
.
Note:
Assume no material is wasted.
The answer is 22.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Volume of the cube:
V c u b e = 6 3 = 2 1 6
Surface area of the cube:
S c u b e = 6 ( 6 2 ) = 6 ( 3 6 ) = 2 1 6
The cube and cuboid must have equal volumes:
V c u b o i d = 1 8 ( 6 ) h
2 1 6 = 1 0 8 h
h = 2
Therefore, the dimension of the cuboid is 1 8 × 6 × 2 . And surface area is
S c u b e = 2 [ 2 ( 1 8 ) + 2 ( 6 ) + 1 8 ( 6 ) ] = 2 ( 1 6 0 ) = 3 1 2
The ratio of the surface areas is,
r a t i o = 3 1 2 2 1 6 = 1 3 9
Finally,
a + b = 9 + 1 3 = 2 2