Cubic Tank
A water tank, in the shape of a cube of side length 1 0 0 cm , rests on a flat ground on one of its faces.
It is filled with water to a height of 4 0 cm . Then the tank is tilted and rotated such that its major diagonal is vertical. That is, the tank is now resting on one of its vertices A, with the opposing vertex B directly above it.
How high above vertex A is the water now?
Enter your answer in centimeters, rounded to the nearest hundredth of a centimeter.
The answer is 78.84.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
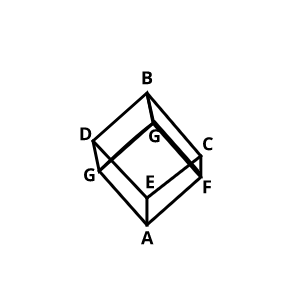First we split the cube to 3 parts, the triangle at the upper(GDCB) and lower part(GEFA), and the middle part(GDCEGF).
We can easily calculate the volume of the whole body which is
1
0
0
3
.
The side length of the triangles are 100 cm, so the base area is
8
6
6
0
.
2
5
4
c
m
2
, the
height of 1 triangle is 57.735 cm
so the volume of one triangle is
1
6
6
6
6
6
.
5
8
8
2
3
c
m
3
.
With these, you can calculate the volume of the middle part, which is
1
0
0
3
−
2
∗
1
6
6
6
6
6
.
5
8
8
2
3
=
6
6
6
6
6
6
.
8
2
3
5
4
c
m
3
.
We know the
height of this part
substracting 2 times the triangle height from the major diagonal, so it'll be
57.735 cm
.
We also need the total volume of the water in the cube which is
1
0
0
2
∗
4
0
c
m
3
.
Because the volume of the water is less than the volume of a triangle and the middle part, the top level will be in this part.
The total water in this part is
4
0
0
0
0
0
c
m
3
−
1
6
6
6
6
6
.
5
8
8
2
3
c
m
3
=
2
3
3
3
3
3
.
4
1
1
7
7
c
m
3
.
Notice an important thing, that as the water level increases in the middle part, the volume of the water is increasing evenly (the area of any horizontal section is equal).
Calculate the ratio, that what percent of this middle body is water. We get
2
3
3
3
3
3
.
4
1
1
7
7
/
6
6
6
6
6
6
.
8
2
3
5
4
=
3
5
%.
Now we have the water level in the middle part as:
5
7
.
7
3
5
/
0
.
3
5
=
2
0
.
2
0
7
2
5
.
Now we add the two heights
2
0
.
2
0
7
2
5
+
5
7
.
7
3
5
=
7
7
.
9
4
2
2
5
c
m
, which is our answer.
(The official answer is not the same because of rounding)