Cubics, Rectangles and Parallelograms.
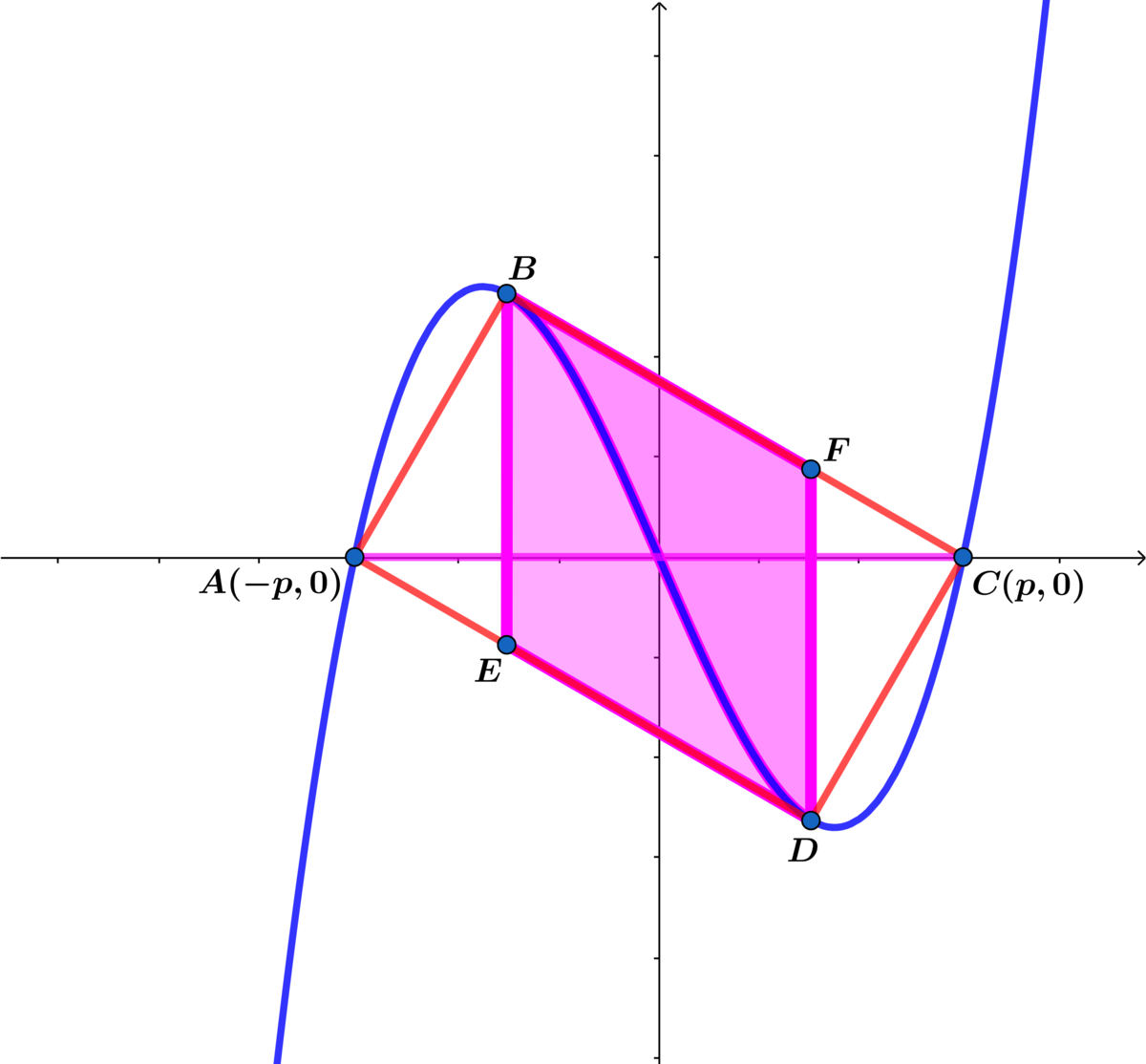
The graph of the cubic function above has has real roots at and and the lines and are tangent to the curve at and respectively.
If the two tangent points and two non-zero -intercepts are joined together to rectangle and the area of parallelogram is , where and are coprime positive integers, find .
The answer is 11.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
m ( x ) = x ( x − p ) ( x + p ) = x 3 − p 2 x ⟹ d x d m ∣ x = x 0 = 3 x 0 2 − p 2 = x 0 − p x 0 ( x 0 − p ) ( x 0 + p ) ⟹
3 x 0 2 − p 2 = x 0 + p x 0 ⟹ 2 x 0 2 − p x 0 − p 2 = 0 ⟹ x 0 = p , − 2 p
x 0 = p ⟹ x 0 = − 2 p ⟹ B : ( − 2 p , 8 3 p 3 ) and D : ( 2 p , − 8 3 p 3 ) .
A C = B D = 2 p = 4 p 1 6 + 9 p 4 ⟹ 6 4 = 1 6 + 9 p 4 ⟹ p 4 = 3 1 6 ⟹ p = 4 3 2 .
To obtain the area of parallelogram B F E D you can:
(1) Find the area of the region bounded by the line the curve m ( x ) = x 3 − 3 4 and the line y = − 3 1 x − 4 2 7 2 then double the result.
Or
(2) Use slopes and distances to find the area.
Using (1):
A ( − 4 3 2 , 0 ) , D ( 4 3 1 , − 4 3 )
⟹ m A D = − 3 1 ⟹ y = − 3 1 x − 4 2 7 2 = n ( x )
and,
m ( x ) = x 3 − 3 4 x
⟹ A 1 = A 2 = ∫ − 4 3 1 4 3 1 m ( x ) − n ( x ) d x =
∫ − 4 3 1 4 3 1 ( x 3 − 3 x + 3 4 3 2 ) d x = 4 x 4 − 2 3 x 2 + 3 4 3 2 x ∣ − 4 3 1 4 3 1 = 3 4
⟹ A B F E D = 3 8 = b a ⟹ a + b = 1 1 .
Using (2) :
m A D = m B C = − 3 1 .
For A D : y = − 3 1 x − 4 2 7 2
For ⊥ line F G that passes thru F : ( 4 3 1 , 4 2 7 1 ) :
m ⊥ = 3 ⟹ y = 3 x − 4 2 7 2 ⟹ 3 x − 4 2 7 2 = − 3 1 x − 4 2 7 2 ⟹ x = 0 ⟹ y = − 4 2 7 2
⟹ G F = 4 2 7 2 and E D = B F = 4 2 7 4 ⟹
A B F E D = 3 4 1 2 ∗ 3 4 3 4 = 3 8 = b a ⟹ a + b = 1 1 .