Turning Cuboids Into A Cube
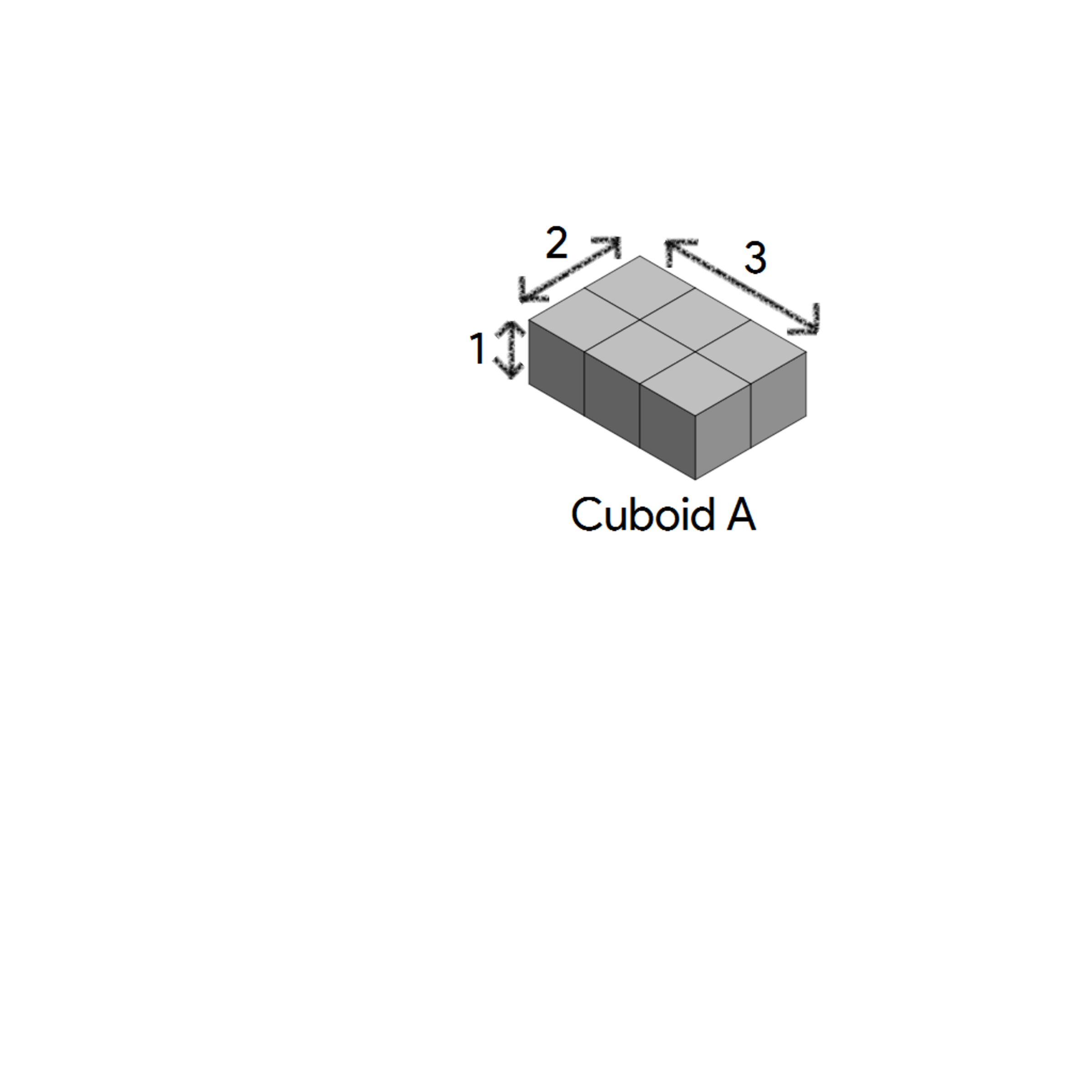
cuboid 's are arranged to form the smallest cube possible.
Find the total surface area of the cube.
The answer is 216.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Side of the cube formed by N cuboid As = LCM of 1 , 3 , 2 = 6 units
Surface Area of the cube = 6 × ( 6 ) 2 = 2 1 6 unit 2