Cunning Complex 4

By letting z = a + bi and using the givens above, [z - z(1)]/[z - z(2)] = [(a^2 + b^2 - 14a - 12b + 76) + i(6b - 36)]/[a^2 - 8a + b^2 - 12b + 52].

From here, arg([z - z(1)]/[z - z(2)]) = arctan([6b - 36]/[a^2 + b^2 - 14a - 12b + 76]) = pi/4, which implies that (a - 7)^2 + (b - 9)^2 = 18.

Hence, |z - 7 - 9i| = |(a - 7) + i(b - 9)| = sqrt[(a - 7)^2 + (b - 9)^2] = sqrt(18).

In this solution I am going to use a geometrical approach. In the following graph the point $A$ represents the complex number $z_{2}$ , $B$ represents $z_{1}$ , $C$ the number $7+9i,$ and $D$ the number $z$

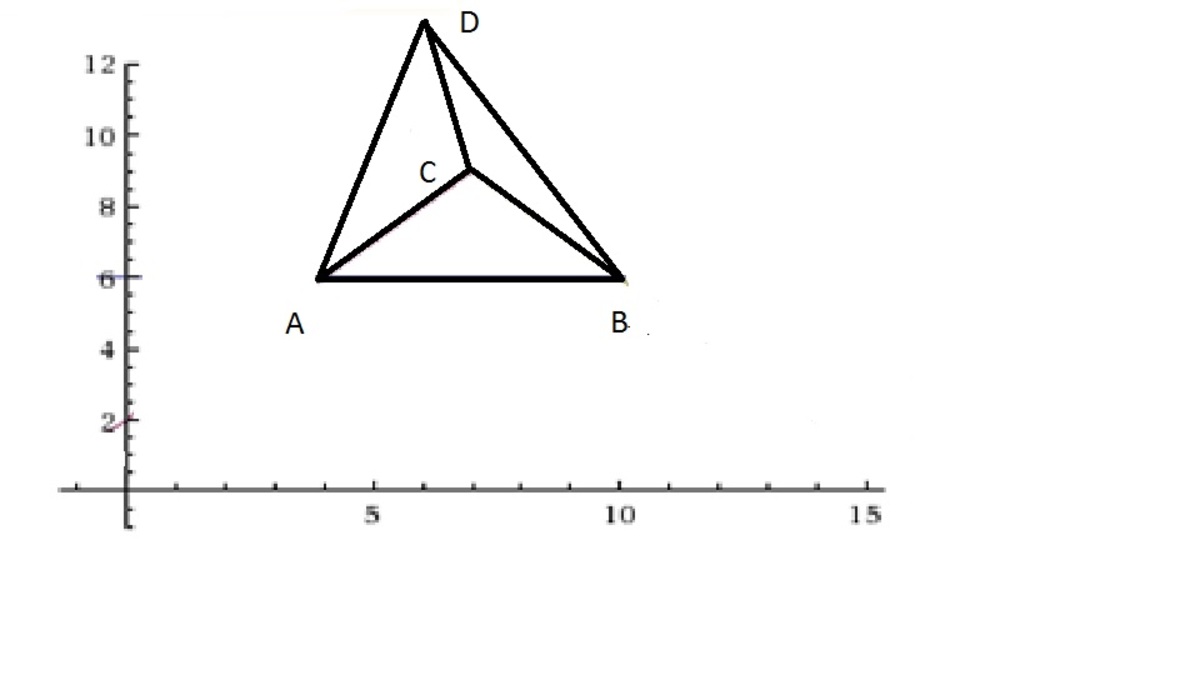
The slope of the segment $AC$ is $1,$ and the slope of the segment $CB$ is $-1.$ Therefore, the angle $ACB$ is $90^{o}$ . It is also easy to verify that $\overline{AC}=\overline{CB}=3\sqrt{2}.$ Since $ADB=\arg {(z-z_{1})} -\arg{(z-z_{2})}=\arg\frac{z-z_{1}}{z-z_{2}}=45^{o}$ , then $ADB=\frac{1}{2} ACB$ . Thus $D$ belongs to the circle with center at $C$ and radius $3\sqrt{2}$ and therefore $|z-7-9i|=\overline{DC}=3\sqrt{2}\approx 4.242.$

Note: We consider only the case when $D$ is above the horizontal line passing through $A$ and $B$ , because if $D$ is below that line then it easy to see that $\arg\frac{z-z_{1}}{z-z_{2}}=\arg {(z-z_{1})} -\arg{(z-z_{2})}<0,$ and therefore is never going to be equal to $45^{o}.$

Same method as John Ashley Capellan in $LaTex$ .

Let $z=a+bi$ and $f(z) = \dfrac {z-z_1}{z-z_2}$ . Then:

$\begin{aligned} f(z) & = \dfrac {a-10+(b-6)i}{a-4+(b-6)i} \\ & = \dfrac {[(a-10)+(b-6)i][(a-4)-(b-6)i]}{[(a-4)+(b-6)i][(a-4)-(b-6)i]} \\ & = \dfrac{(a-10)(a-4)+(b-6)^2 -(a-10)(b-6)i+(a-4)(b-6)i}{(a-4)^2+(b-6)^2} \\ & = \dfrac{a^2-14a+40+b^2-12b+36 +(b-6)(-a+10+a-4)i}{(a-4)^2+(b-6)^2} \\ & = \dfrac{(a^2-14a+b^2-12b+76) +6(b-6)i}{(a-4)^2+(b-6)^2} \end{aligned}$

For $\arg {\left(f(z)\right)} = \frac{\pi}{4} \quad \Rightarrow \Re{(f(z))} = \Im{(f(z))}$

$\begin{aligned} \Rightarrow a^2-14a+b^2-12b+76 & = 6(b-6) \\ a^2-14a+b^2-12b+76 - 6b+36 & = 0 \\ a^2-14a+b^2-18b+112 & = 0 \\ (a-7)^2 - 49 +(b-9)^2 - 81 +112 & = 0 \\ (a-7)^2 + (b-9)^2 & = 18 \\ \Rightarrow |z-7-9i|^2 & = 18 \\ |z-7-9i| & = \boxed{\sqrt{18}} \end{aligned}$

Prerequisite :

$\arg\left(\dfrac{z-z_{1}}{z-z_{2}}\right) = \theta$ Represents,
1) Major arc of a circle passing through $z_{1}$ and $z_{2}$ when $\theta < \dfrac{\pi}{2}$
2) Semicircle when $\theta = \dfrac{\pi}{2}$
3) Minor arc when $\theta > \dfrac{\pi}{2}$

Solution :

Let the centre of the circle be P $( a, b)$ and the variable point be A $(x,y)$
The points $z_{1}$ and $z_{2}$ lie on the circle.Thus they are equidistant from the centre. Hence, the centre lies on the perpendicular bisector of line joining them, which is
$Re(z) = 7$
Hence, $a = 7$

Now, draw four lines joining the variable point & centre with $z_{1}$ and $z_{2}$ as shown. ( Will post the image later. )

We know that the angle formed by the arc at centre is twice the angle formed by the arc at the circumference.

$\therefore \angle z_{1}Pz_{2} = 2\angle z_{1}Az_{2}= \dfrac{\pi}{2}$
Thus the centre lies on the circle formed with $z_{1}z_{2}$ as diameter.
Radius of this circle $= \left|4+6\iota - (7+6\iota) \right | = 3$

Distance $z_{1}P = \left | A - P \right | = \left |z_{1} - P \right| = \sqrt{3^{2}+3^{2}} = 3\sqrt{2}$