Cupid's Arrows
x 2 + ( 4 5 y − ∣ x ∣ ) 2 = 1 .
A 1- T magnetic field is directed towards and parallel to the positive z -axis. Determine the magnetic flux (in W b , to the nearest tenths) of the area enclosed by the equation above.
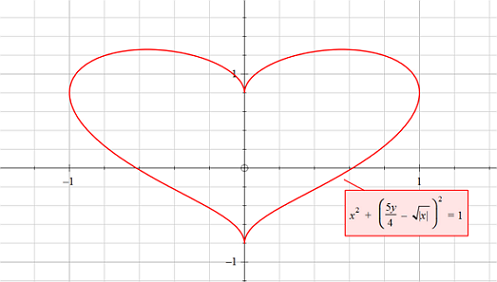 Plot of the equation above
Plot of the equation above
Details and Assumptions :
-
Assume that 1 unit is equivalent to 1 meter.
-
T stands for Tesla, the unit of magnetic field strength.
The answer is 2.5.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
But why do you take ∫ − 1 1 ( P 1 − P 2 ) d x .
Shouldn't it be ∫ − 1 1 ( P 1 + P 2 ) d x
Thanks!
Log in to reply
To get the area enclosed by two curves, the "lower function" is subtracted from the "upper function"...
If one does the latter part, it's simply adding the area enclosed by each function and the x-axis (and there are two x-intercepts to consider!) which is outside the enclosed area as defined by the problem.
Log in to reply
Aha! I had not quite understood the solution then! I do now. Thanks!
Φ = B ⊥ A , and with B ⊥ = 1 Wb/m 2 this problem is equivalent to asking for the area.
The trick is to ignore the ∣ x ∣ term. Without it, the equation describes an ellipse. With the term, each vertical "strip" of the area is shifted upward without affecting its length.
So I look at x 2 + ( 4 5 y ) 2 = 1 and recognize is as the equation of an ellipse. Its extreme points are when x 2 = 1 and ( 4 5 y ) 2 = 1 , so it follows that the semimajor and semiminor axes have lengths a = 1 and b = 5 4 respectively.
The area of an ellipse is A = a b π = 1 ⋅ 5 4 ⋅ π ≈ 2 . 5 1 3 .
I used integration but is a long and inelegant process. I find your trick very interesting.. But I don't understand why ignoring the sqrt(abs(x)) term we obtain an ellipse which has the same area of the first surface. Please, could you explain me this? Thanks! :D
Log in to reply
Consider a small vertical strip of the area, at horizontal position x and of width d x , between y 1 and y 2 . The area of this strip is d A = ( y 2 − y 1 ) d x .
If I replace y 1 and y 2 by y 1 + f ( x ) and y 2 + f ( x ) , the strip is shifted vertically but the its area remains the same. Applying this to all strips, the total area remains the same.
Now choose f ( x ) = 5 4 ∣ x ∣ , and you apply this transformation. You'll find that x 2 + ( 4 5 y − ∣ x ∣ ) 2 = 1 is transformed into x 2 + ( 4 5 y ) 2 = 1 .
Log in to reply
So great observation.. Perfect! Is completely clear. Thank you so much.
Absolutely Wonderful and beautiful method sir
But a doubt,
Isn't magnetic flux Φ B equal to Φ B = ∮ P B ⋅ d ℓ
Log in to reply
No, it's Φ B = ∫ S B ⋅ d S . The expression you mention plays a role in Ampere's law: ∮ C B ⋅ d ℓ = μ 0 ∫ S I ⋅ d S .
Log in to reply
OK thanks. I just took it analogues to Gauss Law.
This problem is quite mathematical, actually.
The magnetic flux is calculated by the following formula:
ϕ = B ⋅ A
With B given, there is a need to evaluate A .
Rearranging the given equation eventually leads to two equations:
y = 5 4 ( ∣ x ∣ + 1 − x 2 ) and y = 5 4 ( ∣ x ∣ − 1 − x 2 )
Evaluating the area via definite integrals,
∫ − 1 1 5 4 ( ∣ x ∣ + 1 − x 2 ) − 5 4 ( ∣ x ∣ − 1 − x 2 ) d x
∫ − 1 1 5 8 ( 1 − x 2 ) d x
5 8 ⋅ 2 π
2 . 5
Substituting back to the formula for magnetic flux results in 2 . 5 Wb.