Curious Balance
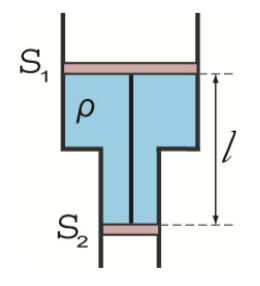
Two cylindrical tubes are joined and placed vertically in the earth's gravitational field. Inside the tubes, there is water enclosed between two pistons which are tied by an inextensible string. The masses of the pistons and the string are negligible and there is no friction between the pistons and the walls. The ends of the tubes are open to the atmosphere, and the whole system remains at rest.
Find the tension of the string in Newtons , knowing that and the density of water is .
Bonus : test your expressions by studying how they behave when .
The answer is 45.78.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
P a t m ⋅ S 1 + T − P 1 ⋅ S 1 = 0 P a t m ⋅ S 2 + T − P 2 ⋅ S 2 = 0
Because of hydrostatic pressure, P 2 = P 1 + ρ g l
Solving for P 1 , P 2 and T is quite straightforward:
P 1 = P a t m + ρ g l ⋅ S 1 − S 2 S 2 P 2 = P a t m + ρ g l ⋅ S 1 − S 2 S 1 T = ρ g l ⋅ S 1 − S 2 S 1 ⋅ S 2
Note that T is not affected by the atmospheric pressure and that the string makes P 1 and P 2 dependent on all the parameters of the system.
The numerical values given yield T = 1 0 3 m 3 kg ⋅ 9 . 8 1 s 2 m ⋅ 0 . 3 5 m ⋅ 0 . 0 4 m 2 − 0 . 0 1 m 2 0 . 0 4 m 2 ⋅ 0 . 0 1 m 2 = 4 5 . 7 8 N
When S 2 ≪ S 1 ⟹ P 1 ≈ P a t m , P 2 ≈ P a t m + ρ g l and T ≈ ρ g l S 2 . In this case, the upper piston is unaffected by the pull of the string and the tension must balance only the force exerted by the hydrostatic pressure on the lower piston.