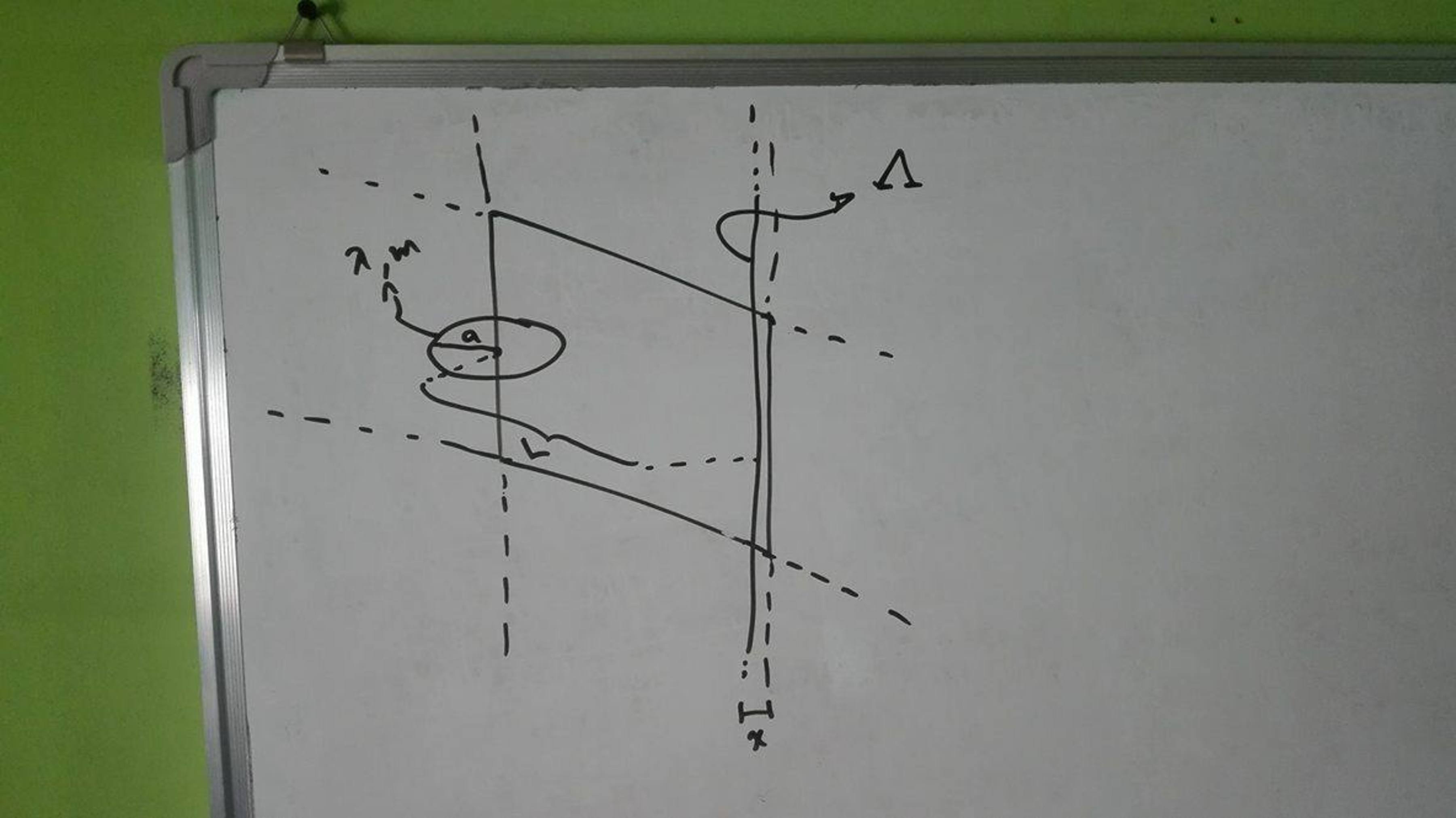
Current?

As there is a conductor plane, it works as a Faraday Cage . So, only half of the ring is affected by the Electric Field of the line, producing a Torque on the ring and making it rotate. As we know: $i=\frac{dq}{dt}=\frac{\lambda dl}{dt}=\lambda a \frac{d\theta}{dt}=\lambda a \dot{\theta}$ As $x<<a$ we can approach it to be on the plane, but always affecting only half of the ring. As $a<<L$ the electric field made by the line tends to be constant at each point on the ring, so, by Gauss's Law : $\iint_{S}\vec{E}\cdot d\vec{A}=\frac{Q_{enclosed}}{\epsilon_{0}}\Rightarrow E=\frac{\Lambda}{2\pi L \epsilon_{0}}$ And, by using the equation of torque: $I\ddot{\theta}=a\cdot E\cdot Q_{ring}\Rightarrow ma^2\ddot{\theta}=\frac{a^2\lambda \Lambda}{2L\epsilon_{0}}$ $\Rightarrow \ddot{\theta}=\frac{\lambda \Lambda}{2mL\epsilon_{0}} \Rightarrow \dot{\theta}=\frac{\lambda \Lambda t}{2mL\epsilon_{0}}$ $\Rightarrow i=\frac{\lambda^2 a \Lambda t}{2mL\epsilon_{0}} \Rightarrow \Lambda=\frac{2mL\epsilon_{0}i}{\lambda^2 at}$