Current round Cone!
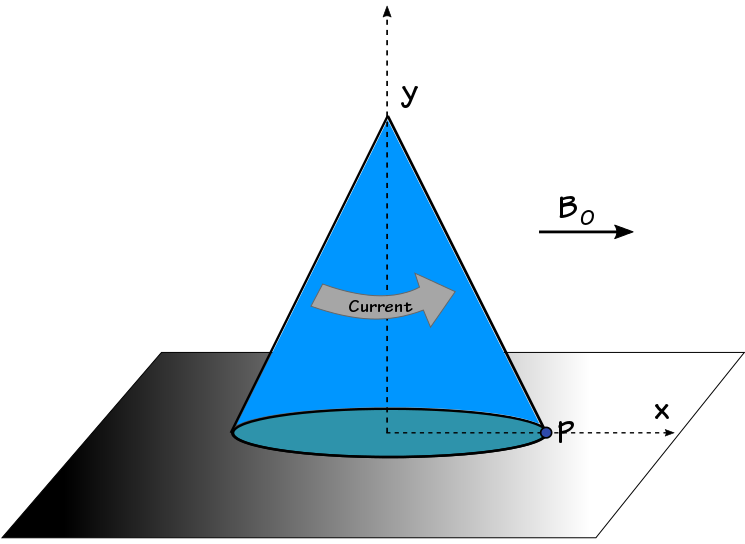
A cone mass , radius , and height has a current flowing uniformly along its curved surface area. This cone is kept on a rough surface in a magnetic field .
If the maximum value of current such that the cone doesn't topple about point is determine the value of .
The answer is 2.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Relevant wiki: Magnetic Moment
Two torques are acting on the cone, one is due to the gravitational force and second is due to the magnetic field. The torque of gravity is acting anticlockwise about the point P and trying to keep the cone in its position while the torque of magnetic field is acting in clockwise direction and trying to topple it.
To calculate the torque due to magnetic field, the cone can be imagined as made up of large many small current carrying rings. Each ring a can treated as a magnetic dipole and the net magnetic dipole moment of the cone can be calculated by adding the magnetic moments ( i × A ) of these individual rings.
Once magnetic moment of the cone is calculated, torque can be found out as τ = M × B
Now, imagine a ring of width dx at a depth x from the apex as shown below.
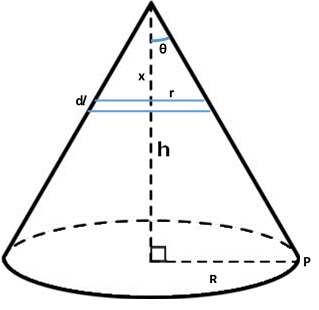
The current flowing in this ring can be calculated by unitary method.
di = curved surface area of cone total current × area of the ring
The area of the ring is π r d l
di = π R L i × 2 π r d l
Here, L is the slant height.
d l cos θ = d x
Also, tan θ = r x = R h
The magnetic dipole moment (dM) of the elemental ring assumed is d M = d i × Area of the loop
Therefore,
M = ∫ 0 h ( π R L i 2 π h R x cos θ d x ) × π ( h R x ) 2
M = 2 i π R 2
The direction of the magnetic dipole moment can be calculated by the right hand rule as vertically upwards.
Torque due to magnetic field on the cone will be given by
τ = M B sin θ
The direction of this torque will be into the plane and will try to rotate the cone clockwise.
To prevent toppling, the torque of magnetic field should not exceed the torque of gravity about the point P,
Therefore,
2 i π R 2 B 0 sin 9 0 ∘ = m g R
i = π R B 0 2 m g
Hence, the answer is 2.