Does A Protractor Help?
Calculus
Level
2
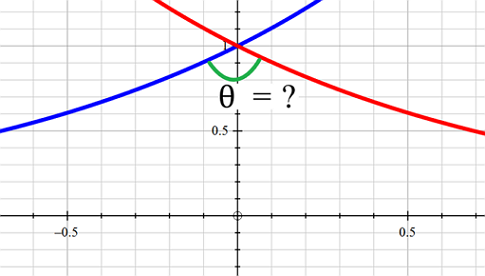
What can we say about these two curves:
They intersect at
and have an acute angle at the point of intersection
They intersect at
and create a right angle at the point of intersection
They intersect at
and have an obtuse angle at the point of intersection
They do not intersect
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
If y 1 = e x and y 2 = e − x intersect then y 1 = y 2 or
e x e 2 x 2 x ⟹ x ⟹ y 1 = e − x = 1 = ln 1 = 0 = 0 = y 2 = e 0 = 1 .
The two curves intersect at ( 0 , 1 ) .
The gradients of the two curves are:
⎩ ⎪ ⎨ ⎪ ⎧ d x d y 1 ∣ ∣ 0 d x d y 2 ∣ ∣ 0 = e x ∣ ∣ 0 = − e − x ∣ ∣ 0 = 1 = − 1
therefore, the two curves are perpendicular at the intersection.
That is:
They intersect at (0,1) and created a right angle at the point of intersection.