Looks Like Part Cardioid!
The equation of the circle below is The dot moving along the -axis keeps track of the nearest point on the circle and the corresponding, mirror-image, equidistant point inside the circle. The red, ribbon-shaped figure traces out the path of this latter point.
Compute the area of the O-shaped region enclosed by the red curve, to 3 decimal places.
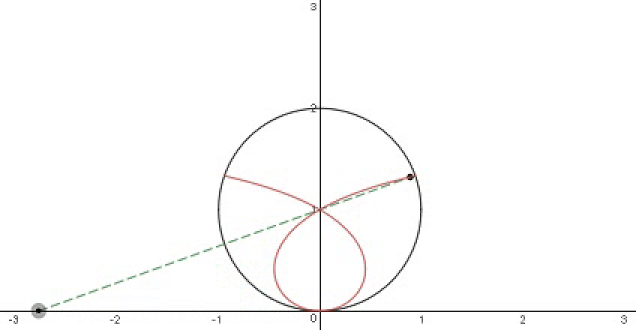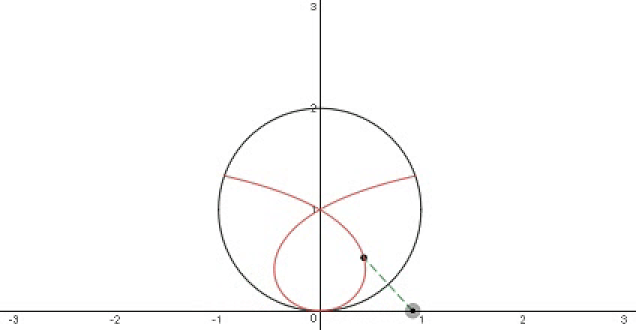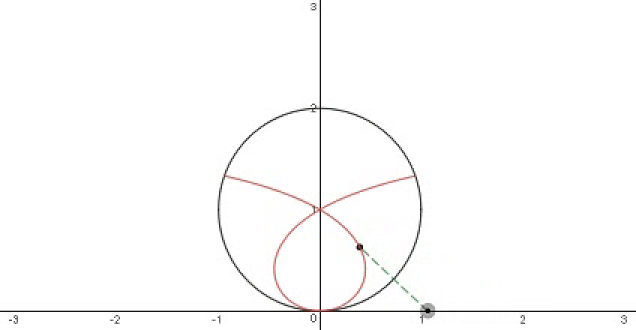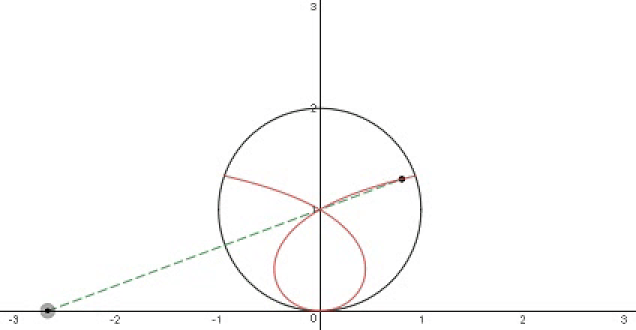
The answer is 0.653.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
There is probably a faster solution than this one.
Let us define the moving point as ( t , 0 ) , where we change t as we choose. The shortest distance between the moving point and the bottom half of the circle can be found by minimizing the function:
d ( x ) = ( x − t ) 2 + ( − 1 − x 2 + 1 ) 2
This can be done by taking the derivative and setting it equal to 0.
0 0 0 t t 2 x 2 t 2 x d ( 1 + t 2 t 2 ) = 2 ( x − t ) + 2 ( − 1 − x 2 + 1 ) ⋅ ( 1 − x 2 x ) = x − t − 1 − x 2 x 1 − x 2 − x = x − t − x + 1 − x 2 x = 1 − x 2 x = 1 − x 2 x 2 = t 2 − x 2 t 2 = x 2 ( 1 + t 2 ) = 1 + t 2 t 2 = t 2 + 1 − 1
This is the distance from the moving point to the circle. If we make another circle ( x − t ) 2 + y 2 = ( t 2 + 1 − 1 ) 2 ), we see that this and the given circle intersect at one point. This new circle will be called circle 1.
{ y = − 1 − x 2 + 1 y = ( t 2 + 1 − 1 ) 2 − ( x − t ) 2
− 1 − x 2 + 1 2 − x 2 − 2 1 − x 2 2 − x 2 − 2 1 − x 2 − 2 1 − x 2 1 − x 2 1 − x 2 0 x = ( t 2 + 1 − 1 ) 2 − ( x − t ) 2 = ( t 2 + 1 − 1 ) 2 − ( x − t ) 2 = t 2 + 2 − 2 t 2 + 1 − x 2 + 2 x t − t 2 = − 2 t 2 + 1 + 2 x t = t 2 + 1 − x t = t 2 + 1 − 2 x t t 2 + 1 + x 2 t 2 = x 2 ( t 2 + 1 ) − x ⋅ 2 t t 2 + 1 + t 2 = t 2 + 1 t t 2 + 1
Plugging in this x value into the equation of the bottom half of the given circle, we get that the point of intersection of the two circles is ( t 2 + 1 t t 2 + 1 , − 1 + t 2 1 + 1 ) .
The mirror image of the moving point will be on the circle ( x − t ) 2 + y 2 = 4 ( t 2 + 1 − 1 ) 2 , as it has twice the radius of circle 1. We will call this circle 2.
The line through the center of circle 2 and the point of intersection we found earlier is y = 1 − t x .
Now we need to find the intersection of circle 2 and this line. After solving this system of equations in a similar way as before, we get that the line and circle 2 intersect at ( t 2 + 1 2 t t 2 + 1 − t , 2 − t 2 + 1 2 t 2 + 1 ) . This is exactly the parametric form of the ribbon shaped curve.
The curve has a vertical tangent when t = 2 3 2 − 1 . The curve intersects the y -axis at t = 0 and t = 3 .
If we say that f ( t ) = t 2 + 1 2 t t 2 + 1 − t and g ( t ) = 2 − t 2 + 1 2 t 2 + 1 , the area of the loop is
2 ( ∫ 3 2 3 2 − 1 g ( t ) f ′ ( t ) d t − ∫ 0 2 3 2 − 1 g ( t ) f ′ ( t ) d t ) = 0 . 6 5 3