Cut Cube Surface Area
A unit cube is to be cut by a plane defined by three points that it passes through. The cube faces are parallel to the coordinate planes, with one vertex at the origin and the opposing vertex at ( 1 , 1 , 1 ) . The cutting plane passes through the points ( 0 . 5 , 0 , 1 ) , ( 0 , 0 . 5 , 1 ) and ( 1 , 1 , 0 . 5 ) . Find the total surface area of the portion of the cube that will separate upward when the cut is complete (the upper part of the cube).
If this area can be expressed as d a + b c , for coprime integers a , b and d , and square-free integer c , then find a + b + c + d
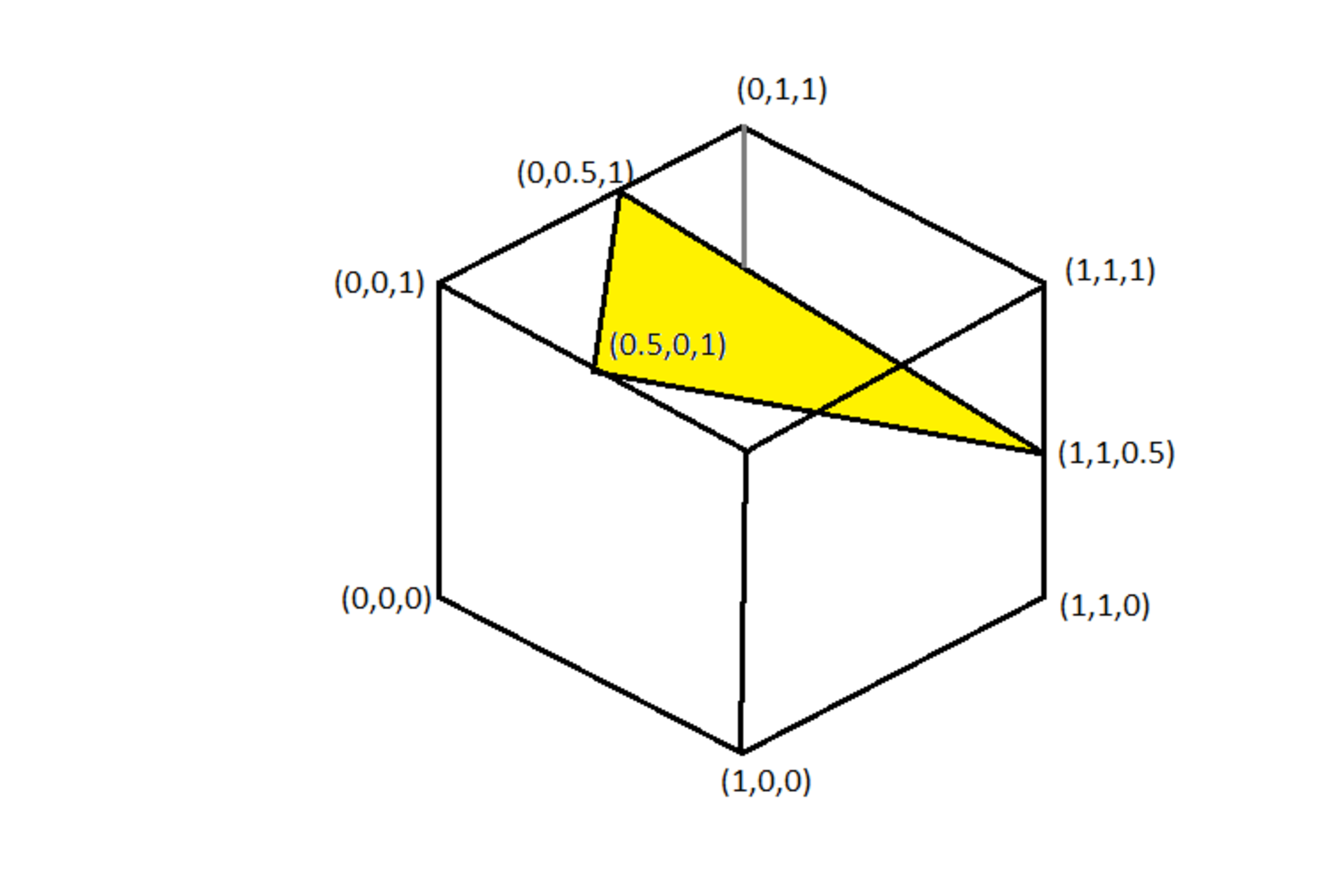
The answer is 81.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Label the diagram as follows:
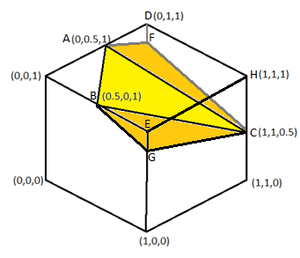
The plane has an equation of x + b y + c z = d , and since it goes through A ( 0 , 2 1 , 1 ) , B ( 2 1 , 0 , 1 ) , C ( 1 , 1 , 2 1 ) , we know that 0 + 2 1 b + c = d , 2 1 + 0 + c = d , and 1 + b + 2 1 c = d , which solves to b = 1 , c = 3 , and d = 2 7 , and gives an equation of x + y + 3 z = 2 7 or 2 x + 2 y + 6 z = 7 .
G is also on the plane 2 x + 2 y + 6 z = 7 with x = 1 and y = 0 , so its coordinates solve to ( 1 , 0 , 6 5 ) , which means E G = 1 − 6 5 = 6 1 .
The area of △ B E G is A △ B E G = 2 1 ⋅ B E ⋅ E G = 2 1 ⋅ 2 1 ⋅ 6 1 = 2 4 1 . By symmetry, A △ A D F = A △ B E G = 2 4 1 .
The area of trapezoid E H C G is A E H C G = 2 1 ( E G + H C ) E H = 2 1 ( 6 1 + 2 1 ) 1 = 3 1 . By symmetry, A D H C F = A E H C G = 3 1 .
The area of △ E D H is A △ E D H = 2 1 ⋅ E H ⋅ D H = 2 1 ⋅ 1 ⋅ 1 = 2 1 .
By the Pythagorean Theorem, the height of trapezoid A D E B is h 1 = B E 2 − ( 2 1 ( D E − A B ) ) 2 = ( 2 1 ) 2 − ( 2 1 ( 2 − 2 2 ) ) 2 = 4 2 . The area of trapezoid A D E B is then A A D E B = 2 1 ( A B + D E ) h 1 = 2 1 ( 2 2 + 2 ) 4 2 = 8 3 .
By the Pythagorean Theorem on △ B E G , B G = B E 2 + E G 2 = ( 2 1 ) 2 + ( 6 1 ) 2 = 6 1 0 . Also by the Pythagorean Theorem, the height of trapezoid A F G B is h 2 = B G 2 − ( 2 1 ( F G − A B ) ) 2 = ( 6 1 0 ) 2 − ( 2 1 ( 2 − 2 2 ) ) 2 = 1 2 2 2 . The area of trapezoid A F G B is A A F G B = 2 1 ( A B + F G ) h 2 = 2 1 ( 2 2 + 2 ) 1 2 2 2 = 8 1 1 .
By the distance formula, G C = 3 1 0 , and by symmetry, F C = G C = 3 1 0 . By Heron's Formula the area of △ G F C is A △ G F C = 6 1 1 .
The total surface area is S = A △ B E G + A △ A D F + A E H C G + A D H C F + A △ E D H + A A D E B + A A F G B + A △ G F C = 2 4 1 + 2 4 1 + 3 1 + 3 1 + 2 1 + 8 3 + 8 1 1 + 6 1 1 = 2 4 3 9 + 7 1 1 . Therefore, a = 3 9 , b = 7 , c = 1 1 , d = 2 4 , and a + b + c + d = 8 1 .
Label the cube as shown. If we look along E ′ C ′ , we note that △ A E E ′ and △ A D D ′ are similar. Then D D ′ E E ′ = A D ′ A E ′ ⟹ E E ′ = A D ′ A E ′ × D D ′ = 3 1 × 2 1 = 6 1 . Then we have C ( 0 , 1 , 6 5 ) and E ( 1 , 0 , 6 5 ) . The the cut out surface is a pentagon A B C D E of the shape of a cut diamond.
We can find the side lengths using the coordinates of the end points by ℓ = ( x 1 − x 2 ) 2 + ( y 1 − y 2 ) 2 + ( z 1 − z 2 ) 2 . And they are A B = 2 1 , B C = E A = 6 1 0 , C D = D E = 3 1 0 , and C E = 2 . We note that the are of the pentagon [ A B C D E ] is the of areas of trapezoid A B C E and △ C D E . From the side view along E C , we note that the height of A B C E , h 1 , and the height of △ C D E , h 2 , are h 1 : h 2 = 1 : 2 . And h 1 + h 2 = ( 4 3 2 ) 2 + ( 2 1 ) 2 = 2 2 1 1 . ⟹ h 1 = 6 2 1 1 and h 2 = 3 2 1 1 . Then the area of pentagon A B C D E is given by:
[ A B C D E ] = [ A B C E ] + [ C D E ] = 2 A B + C E × h 1 + 2 C E × h 2 = 2 1 ( 2 1 + 2 ) 6 2 1 1 + 2 1 × 2 × 3 2 1 1 = 8 1 1 + 6 1 1 = 2 4 7 1 1
Other surface areas of the top part of the cube are:
[ A B C ′ D ′ E ′ ] 2 [ A E E ′ ] 2 [ E ′ E D D ′ ] = 1 × 1 − 2 1 × 2 1 × 2 1 = 8 7 = 2 × 2 1 × 2 1 × 6 1 = 1 2 1 = 2 × 2 6 1 + 2 1 × 1 = 3 2
Therefore the surface area of the top part of the cube is 2 4 7 1 1 + 8 7 + 1 2 1 + 3 2 = 2 4 3 9 + 7 1 1 . ⟹ a + b + c + d = 3 9 + 7 + 1 1 + 2 4 = 8 1 .