Cut Cube
When a cube is cut into 8 smaller cubes, its surface area increases by 2016. Find the volume of the original cube.
Round answer to nearest whole number.
The answer is 6159.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
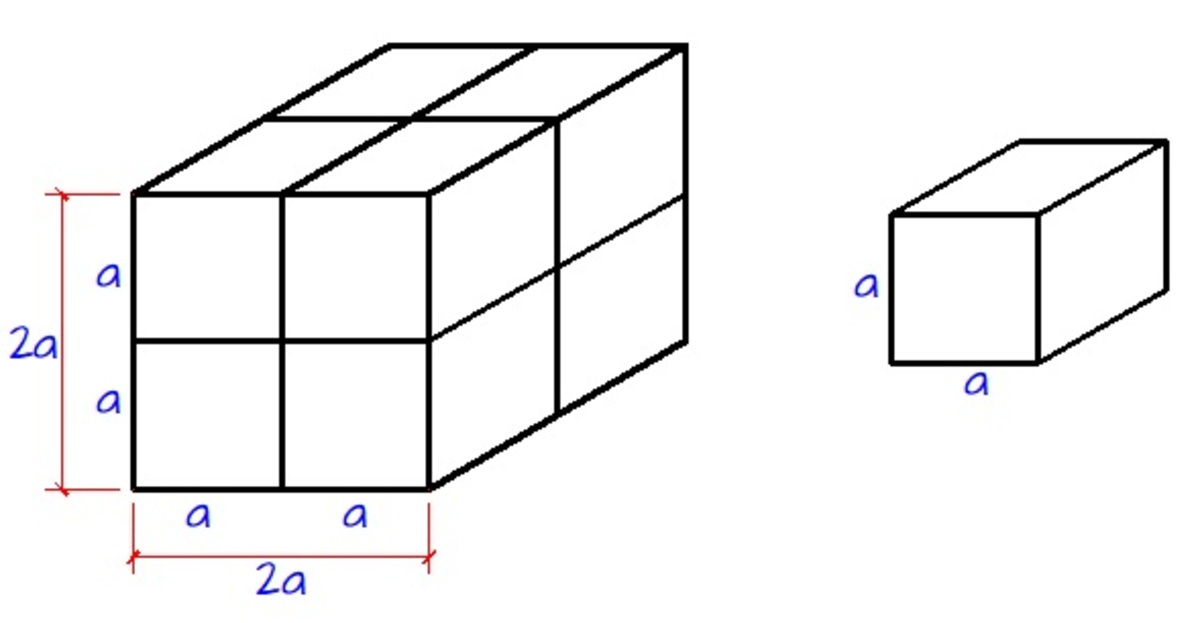 Consider the diagram. Let
S
1
be the surface area of the original cube and
S
2
be the surface area of the
8
small cubes. Then
S
1
=
6
(
2
a
)
2
=
2
4
a
2
and
S
2
=
8
(
6
a
2
)
=
4
8
a
2
. From the problem, it states that
Consider the diagram. Let
S
1
be the surface area of the original cube and
S
2
be the surface area of the
8
small cubes. Then
S
1
=
6
(
2
a
)
2
=
2
4
a
2
and
S
2
=
8
(
6
a
2
)
=
4
8
a
2
. From the problem, it states that
S 2 = S 1 + 2 0 1 6
Substituting, we have
4 8 a 2 = 2 4 a 2 + 2 0 1 6
a 2 = 8 4
a = 8 4 = 2 2 1
The volume of the original cube is
V = ( 2 a ) 3 = ( 4 2 1 ) 3 ≈ 6 1 5 9
Let the edge of larger cube be A and that of smaller cube be a, then by Volume conservation we get A 3 = 8 a 3 or A=2a.
Surface area of larger cube = 6 A 2 = 2 4 a 2 .
Surface area of smaller 8 cubes = 8 ( 6 a 2 ) = 4 8 a 2 .
Now difference of surface areas= 4 8 a 2 − 2 4 a 2 = 2 4 a 2 = 2 0 1 6 ⇒ a = 8 4 Hence volume of larger cube =8( 8 4 ) 3 = 6159...(approximately)