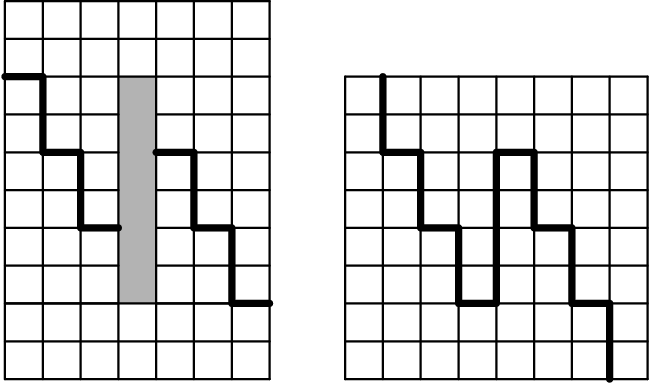cut, cut, cut

Geometry Level 2

There's a 1 × 6 1\times 6 rectangle hole in the middle of a 7 × 10 7\times 10 rectangle.

True or False?

We can cut the holey rectangle into two pieces using straight lines, and rearrange these pieces into a square.

False True

Áron Bán-Szabó by Áron Bán-Szabó , 17, Hungary

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

3 solutions

Jon Haussmann
Sep 2, 2017

1 Helpful 0 Interesting 2 Brilliant 1 Confused
Kenny O.
Sep 14, 2017

A r e a o f h o l e y r e c t a n g l e = A r e o f r e c t a n g l e − h o l e = 7 ∗ 10 − 1 ∗ 6 = 64 Area of holey rectangle= Are of rectangle-hole= 7*10-1*6=64
64 = 8 2 64=8^2 , meaning that we can cut the holey triangle into 64 1 ∗ 1 1*1 squares and rearrange the smaller squares to form a bigger square of 8 ∗ 8 8*8

1 Helpful 0 Interesting 0 Brilliant 0 Confused
Azadali Jivani
Aug 31, 2017

Total area of rectangle = 7 * 10 = 70 Area of rectangle hole = 1 * 6 = 6
70 - 6 = 64
8 * 8 = 64

0 Helpful 0 Interesting 0 Brilliant 0 Confused

This is not enough. You need to show a possible cutting.

Áron Bán-Szabó - 3 years, 9 months ago

I'm really curious to see the solution.

Nick Singer - 3 years, 9 months ago

Yes, it is mathematically possible. But You didn't really give a solution to the "cutting into two" part of the question though.

Shuddhasattwa Guha - 3 years, 9 months ago

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...