Cut it up!
We can cut a square into four smaller squares.
We can also cut it into
ten
squares (not necessarily equally sized).
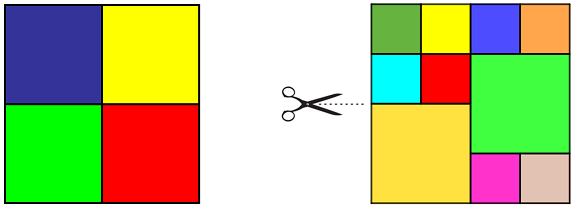However, we can’t cut it up just into
two
, or into
three
squares, without any part of the original square being left over.
If is a (positive integer) number of squares that we cannot obtain by dissecting a square, what is the sum of all possible values of ?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
The side of every square piece is smaller than that of the original square.
Thus, every vertex of the original square must belong to a different square piece.
This makes obvious that we can't have a dissection of only 2 , or 3 , or 5 square pieces.
As seen below, a dissection into 6 , 7 and 8 squares is possible:
Now, notice that every time we cut a square into 4 smaller ones, we augment the total number of pieces by 4 − 1 = 3 .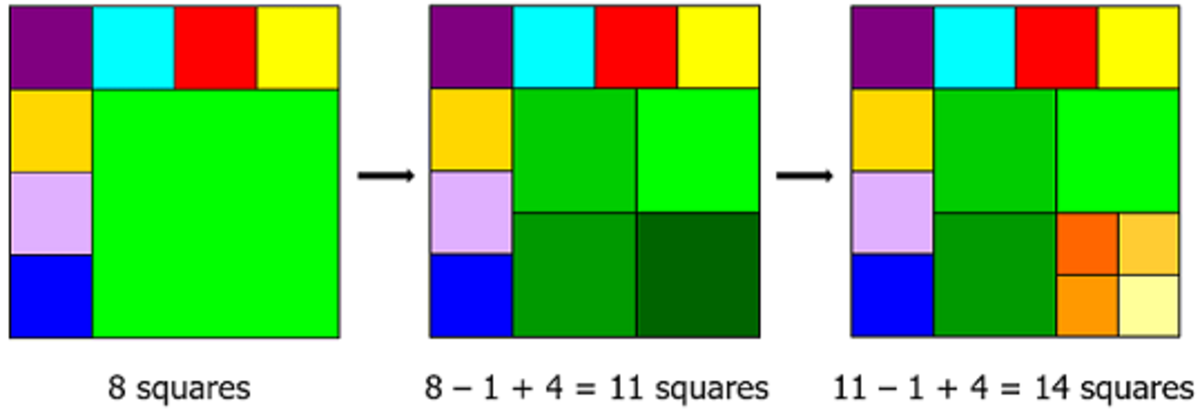
e.g.
and so on…
Thus, we can have dissections where the number of pieces will be of the forms:
6 + 3 n = 3 ( 2 + n ) = 3 m
7 + 3 n = 3 ( 2 + n ) + 1 = 3 m + 1
8 + 3 n = 3 ( 2 + n ) + 2 = 3 m + 2 , for all integers m ≥ 2 .
That means that we can cut the square into any number of square pieces from the set { 4 , 6 , 7 , 8 , 9 , 1 0 , 1 1 , 1 2 , 1 3 , 1 4 , … } .
To conclude, the only numbers of squares we cannot create are k = 2 , k = 3 and k = 5 , hence the sum of the values of k is 2 + 3 + 5 = 1 0 .