Cut the Bridges and Conquer

In the following analysis, we'll assume that the graph is connected. If it is not, we run the algorithm separately for each component.

We could explore our graph using Depth First Search . While doing so, we could think of a spanning tree called the DFS tree . In the DFS tree ,

• $v$ is a child of $u$ if we arrived at $v$ from $u$ while exploring the graph.
• The root is the vertex at which the DFS exploration began.
• If $v$ is a child of $u$ , then $depth[v] = depth[u] + 1$

The non-tree edges are classified into forward edges, backward edges and cross edge depending on the depths they connect.

Consider this graph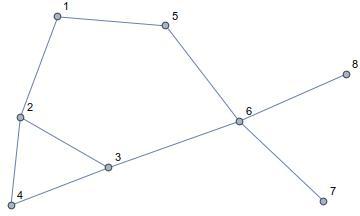 and its corresponding DFS tree

1
2
3
4
5
6
7
8
9

1 -> 2 -> 3 -> 4
          |
          v
     7 <- 6 -> 5
          |
          V
          8

Backedges: 4 -> 2, 5 -> 1

We define a concept called the lowpoint of a vertex. For each vertex $v$ , the lowest depth of neighbors of all descendants of $v$ in the DFS tree is $lowpoint(v)$ . For example, the lowpoint of $2$ in this graph is $d=1$ , since one of its descendants have a backedge to a vertex at depth 1.

Notice that an edge $(u, v)$ is never a bridge if it is not a part of the DFS tree. This is because the DFS tree spans all the vertices in the component, and if there is a way to span $u$ and $v$ without using $(u,v)$ , then $(u,v)$ is redundant.

An edge $u \to v$ on the DFS tree is a bridge if that is the only way to access $u$ from $v$ or vice-versa. This means that there are no back-edges from $v$ to $u$ or its ancestors. Or in other words, $depth[u] < low[v]$

Let's implement that:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29

def getBridges(adjList):
    visited = [False for i in xrange(len(adjList))]
    depth = [0 for i in xrange(len(adjList))]
    low = [0 for i in xrange(len(adjList))]
    parent = [0 for i in xrange(len(adjList))]
    bridges = set()
    def rec(u, d):
        visited[u] = True
        depth[u] = d
        low[u] = d
        childCount = 0
        for v in adjList[u]:
            if not visited[v]:
                parent[v] = u
                rec(v, d+1)
                childCount += 1
                low[u] = min(low[u], low[v])
                if low[v] > depth[u]:
                    bridges.add((u,v))
            elif v != parent[u]:
                low[u] = min(low[u], depth[v])
    for u in xrange(len(adjList)):
        if not visited[u]:
            rec(u,1)
    return bridges

adjList = [[],[14,167],[111,137,160],[31,69,218],[8,14,154,228],[25,92,150,190],[231],[211,223],[4,69,155],[49,161,213,243],[40,172,202],[63,70,101,256],[61,157,261],[173,247],[1,4,77,241,264],[35,138,178],[49,57,250],[],[58,74,150,177,182,201,273],[21,117,244],[54,63],[19,195,229,237],[133,142,188],[48,50,117,155,189,213],[115],[5,85,190,203],[139],[128,130,166,245],[59,133,170],[48],[50,59,236],[3,43,62,151],[192,218,262,267],[61],[51,53,96],[15,59,173,179,182,210],[53,137,143,229],[135,203,265],[52,256,272],[207,233,244],[10,67,79,149],[43,68,119,127,230],[56,62,163],[31,41,73,106,255],[45,224,233,251],[44,70,87,131,175,205,268,272],[50,104,137,165,242],[271,274],[23,29,55,70],[9,16,100,154,226,268],[23,30,46,103,128,216,265],[34,68,230],[38,194,258],[34,36,66,133,150,210,234],[20,174,181,191],[48,246],[42,97,193],[16,114],[18,175,210],[28,30,35,93,100,251,262],[130,149,167],[12,33,115,132,147,214],[31,42,89,151,235],[11,20,110,238,253],[91,104],[72,154],[53,116,235,238],[40,192,236,273],[41,51,106,166],[3,8,193,268],[11,45,48,117,146],[125,224],[65,218,253,262],[43,120,192,238],[18,133,193,197],[],[213],[14,200,254],[96,117,188],[40,91],[167,184,223,236,268],[165],[165,178,182,183,195],[97,274],[152,157],[25,122,162,222],[113,116,209,220,268],[45,99,164,257],[216],[62,101,222,257],[108,252],[64,79,118,162,271],[5,174,269],[59],[96,136,185],[155,160,169,210],[34,78,94,116],[56,83,216],[123,130],[87,103,131,214],[49,59,160,225,254],[11,89,112,138,154,168,260],[130,185,191],[50,99,164,217],[46,64,148,172,202,203],[138,168,217],[43,68,231],[184,187,224],[90,156,177],[247],[63,144,165,257,271],[2,119,202,217,267],[101,140,248,251],[86,129,140,165,218,224],[57,163,190],[24,61],[66,86,96],[19,23,70,78,218,234,264],[91,129,194],[41,111,162,225],[73,221,267],[225],[85,215,245],[98,131,168],[231],[71,204,237],[137,141,158,165],[41,128,135,262,273],[27,50,127,139,266],[113,118,133,182],[27,60,98,102,202,268],[45,99,123,167,238],[61],[22,28,53,74,129,175,235],[],[37,127,159],[94,154,184,242,259,271],[2,36,46,126,226,232],[15,101,105,179,212],[26,128,221],[112,113],[126,224,243,256],[22],[36,168,192,222,234,241],[110,192,211,232,255],[],[70,244],[61,170,174,208,214,256],[104,269],[40,60,268],[5,18,53,156,176,192],[31,62,191,269],[84,185,198],[],[4,49,65,101,136],[8,23,95],[108,150,184],[12,84],[126],[135,196],[2,95,100,233,261],[9,247],[85,91,119,169,240,247],[42,114],[87,103,185],[46,81,82,110,113,126,176,203,253],[27,68],[1,60,80,131,246,253],[101,105,123,143,220],[95,162,192],[28,147,274],[229],[10,104,206],[13,35,200],[54,92,147,196,205,209],[45,58,133,187,237],[150,165],[18,108,237,249,251],[15,82],[35,138,234],[187],[54,221,244],[18,35,82,129],[82],[80,107,136,156,232],[94,102,152,164,192],[245,251],[107,175,180],[22,78],[23,238,268],[5,25,114],[54,102,151],[32,67,73,143,144,150,169,185,246],[56,69,74,231,272,274],[52,118,247,255],[21,82,212,226,237,245,254],[159,174,218],[74,248],[152],[],[77,173,233,241],[18],[10,104,111,130,211,234],[25,37,104,165,246],[125],[45,174],[172,249],[39],[147,217],[86,174,235],[35,53,58,95],[7,144,202,227,234],[138,195,261],[9,23,76],[61,99,147],[122],[50,88,97],[103,105,111,208],[3,32,72,113,117,196,234,250,258],[254],[86,168],[120,139,181],[85,89,143],[7,80],[44,71,107,113,141],[100,119,121],[49,137,195],[211,241,243],[4],[21,36,171],[41,51,270],[6,106,124,193],[137,144,184],[39,44,160,200],[53,117,143,179,202,211,218,239],[62,66,133,209,240],[30,67,80,270],[21,125,175,177,195],[63,66,73,131,189],[234],[162,235],[14,143,200,227],[46,136,265],[9,141,227],[19,39,146,181,251,258],[27,122,186,195,266],[55,167,192,203,250,273],[13,109,161,162,194],[112,197],[177,206,250],[16,218,246,249],[44,59,112,177,186,244],[90],[63,72,165,167,254,264],[77,100,195,219,253,263],[43,144,194],[11,38,141,147],[87,89,110],[52,218,244],[136],[101],[12,160,212],[32,59,72,127,265],[254],[14,117,253],[37,50,242,262],[128,245],[32,111,120],[45,49,69,80,86,130,149,189],[92,148,151],[230,236],[47,91,110,136],[38,45,193,273],[18,67,127,246,272],[47,83,170,193]]

len(getBridges(adjList))

This solution is based on this idea:

We collect all edges $(a, b)$ of the graph, there are 479 of them.

We remove this edge $(a, b)$ from the graph, then if the component containing $b$ does not contain $a$ , this is a bridge.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37

"Cut the Bridges and Conquer"

def initgraph():
    f = open('network-bridge.txt')
    content = f.read().replace('->{',':[').replace('},','],').replace('}}',']}')
    f.close()
    return eval(content)

def component(g, x):
    res = set([x])
    a , b= 0, len(res)
    while a != b:
        news = set()
        for y in res:
            for z in g[y]:
                news.add(z)
        res = res.union(news)
        a , b = b,len(res)
    return res

def getedges(g):
    return [(x,y) for x in g for y in g[x] if x < y]


def solve():
    g= initgraph()
    res = 0
    for (a, b) in getedges(g):
        g[a].remove(b)
        g[b].remove(a)
        if a not in component(g, b):
            res += 1
        g[a].append(b)
        g[b].append(a)
    return res

print(solve())