cute problem

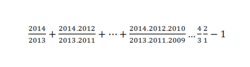
Notice that we can factorise the sum into $\frac{2014}{2013}\left(1+\frac{2012}{2011}\cdots\left(1+\frac21\right)\cdots\right)-1$

Now define then function $f(n)=\frac{2n}{2n-1}(1+f(n-1))$ and let $f(1)=2$ . We can prove that $f(n)=2n$ by induction as follows.

Assume that for some $k$ , $f(k)=2k$ this means that $\begin{aligned} f(k+1)&=\frac{2(k+1)}{2(k+1)-1}(1+f(k))\\ &=\frac{2(k+1)}{2k+1}(2k+1)\\ &=2(k+1) \end{aligned}$

therefore using $f(1)=2$ as a base case we have that $f(n)=2n$ for all positive $n$ .

Now notice the original expression is simply $f(1007)-1$ therefore the answer is $2\times1007-1=2014-2=\boxed{2013}$

Let's do it by construction.

First, define the function f for n even:

$f(2)=\frac{2}{1}$

$f(n)=\frac{n}{n-1}+\frac{n}{n-1}*f(n-1)=\frac{n}{n-1}*(1+f(n-1))$

By induction it's easy to prove that $f(n)=n$

The question asks $f(2014)-1=2014-1=2013$ .