Cutting a cone according to specs !!
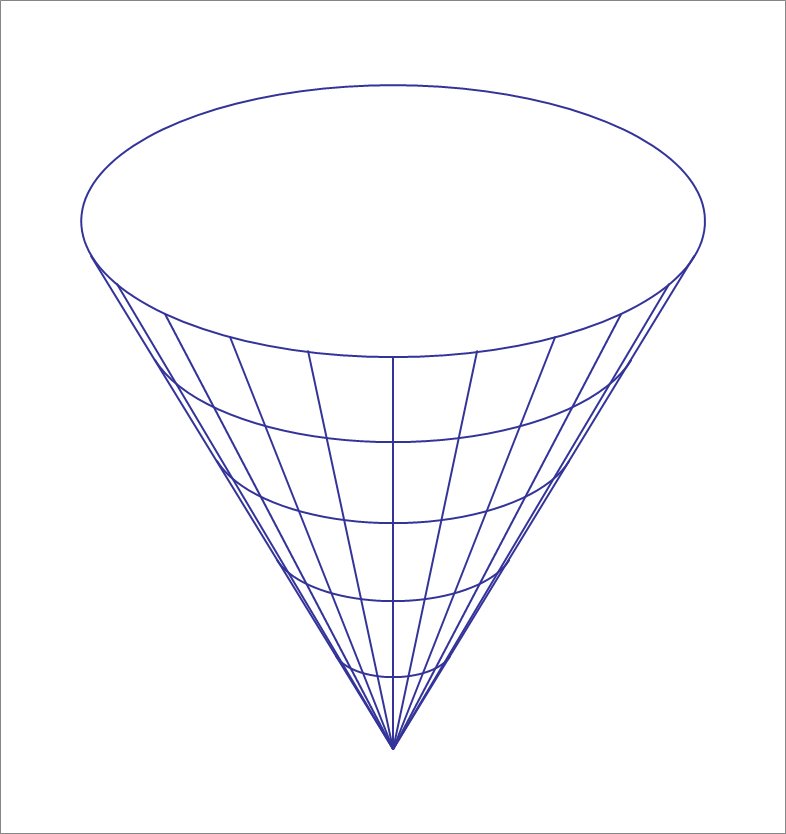
You are given a large solid cone of a semi-vertical angle equal to tan − 1 2 1 , and you are asked to cut the cone to generate an ellipse of semi-minor and semi-major axes lengths equal to 30 cm and 50 cm, respectively. What is the angle ϕ (in degrees) that the cutting plane normal makes with the axis of the cone, and at what distance z 0 from the apex of the cone does it cut the axis of the cone?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Set the origin at the apex, and the z-axis to coincide with the cone axis. The cone has equation 4 x 2 + 4 y 2 = z 2
Intersect the cone with a plane z = a x + b where 0 < a < 2 and b > 0 . Subtitute z, complete the square and rearrange terms to get ( 4 − a 2 x − 4 − a 2 a b ) 2 + 4 y 2 = 4 − a 2 4 b 2
This is an equation of an ellipse, but it is merely the projection of the ellipse onto the x-y-plane. Let's set up coordinates u , v in the plane of intersection. Because the plane has slope a , when x increases by 1 , z increases by a and u increases by 1 + a 2 . We get a coordinate transformation (note that the origin is not at the centre of the ellipse, but we won't need that): u = 1 + a 2 x , v = y
Now y and v reach their extrema when 0 2 + 4 y 2 = 4 − a 2 4 b 2 , so the semi-minor axis is 3 0 = 4 − a 2 b And x and u reach their extrema when y = 0 : ∣ ( 4 − a 2 ) x − a b ∣ = 2 b These are apart by an x-distance of 4 − a 2 4 b which is to be multiplied by a factor 1 + a 2 to get the (spatial) u-distance. The semi-major axis is half of that: 5 0 = 4 − a 2 2 b 1 + a 2
We eliminate b by taking the ratio of the semi axes and solve a = 6 1 8 φ = arctan a ≈ 4 5 ° , 6 8 7 6 b = 6 1 1 8 0 3 0 5 ≈ 5 1 . 5 3 3 9
The eccentricity e of a conic section is e = cos β sin ϕ , where ϕ is the angle that the cutting plane normal makes with the axis of the cone, and β is the semi-vertical angle. The eccentricity of an ellipse is e = 1 − a 2 b 2 , where b is the semi-minor axis and a is the semi-major axis. Therefore, cos β sin ϕ = 1 − a 2 b 2 , and in this problem, cos ( tan − 1 2 1 ) sin ϕ = 1 − 5 0 2 3 0 2 , which solves to ϕ ≈ 4 5 . 6 9 ° , which is sufficient information to choose the correct answer.
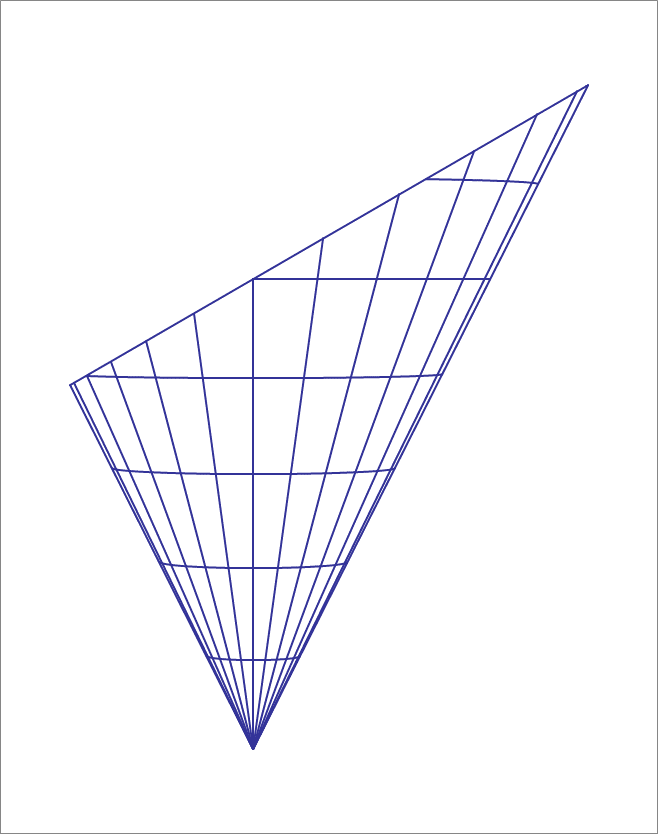
For completeness, the distance z 0 can be found by solving the triangles below from the side view of the conic section, where A is the apex of the conic section, B and C are the intersection points of the ellipse and the surface of the conic section, D is the intersection of the axis of the cone and the cutting plane of the ellipse, and z 0 = A D :
Since B C is twice the semi-major axis, B C = 2 ⋅ 5 0 = 1 0 0 . Since ∠ B A C is twice the semi-vertical angle, ∠ B A C = 2 ⋅ tan − 1 2 1 ≈ 5 3 . 1 3 ° . Since ∠ B D C and ϕ are complementary, ∠ B D C ≈ 9 0 ° − 4 5 . 6 9 ° ≈ 4 4 . 3 1 ° . Then using straight angles and triangle sums, ∠ A D C ≈ 1 3 5 . 6 9 ° , ∠ A B D ≈ 1 0 9 . 1 3 ° , and ∠ A C D ≈ 1 7 . 7 5 ° .
Then using the law of sines on △ A B C , A B sin 1 7 . 7 5 ° = 1 0 0 sin 5 3 . 1 3 ° , which solves to A B ≈ 3 8 . 1 0 .
Finally, using the law of sines on △ A B D , z 0 sin 1 0 9 . 1 3 ° = 3 8 . 1 0 sin 4 4 . 3 1 ° , which solves to z 0 ≈ 5 1 . 5 3 .