Cutting a cone in half
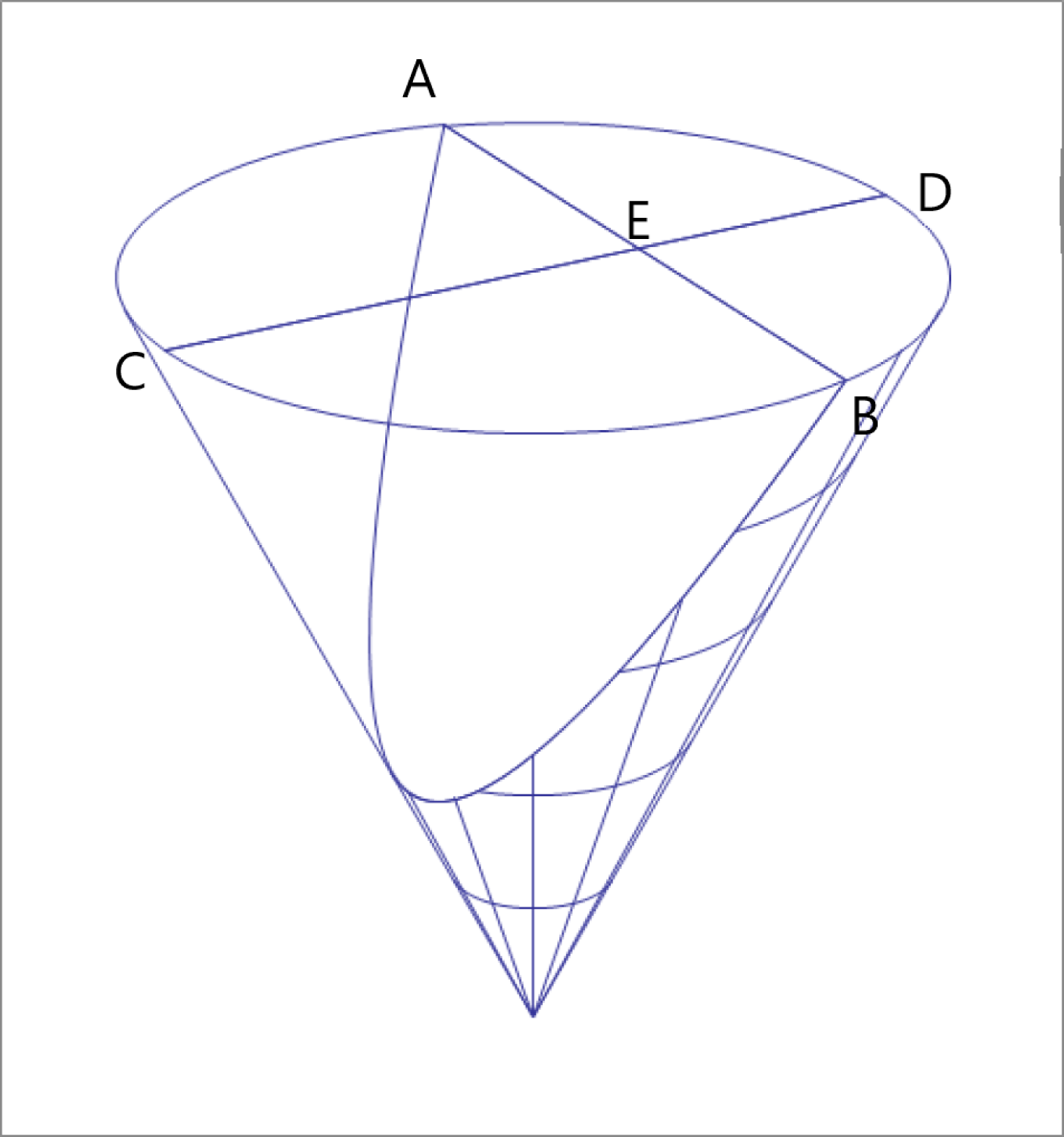
A right circular cone has a base radius of and a height of . You want to cut the cone into two equal volume halves using a parabolic section cut, that is where the cutting plane is parallel to an edge of the cone. If the cutting plane intersects the circular base of the cone in segment , and is the diameter of the base that is the perpendicular bisector of at point , as shown in the figure, then find the length of .
The answer is 6.475.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Let R = 5 be the base radius, and H = 1 0 be the height.
Set up a coordinate system such that the origin is at the apex (bottom).
Equation of cone: r T Q r = 0
with Q = diag { cos 2 θ , cos 2 θ , − sin 2 θ }
, where tan θ = H R = 2 1
Now the cutting plane passes through r 0 = ( r 1 , 0 , H ) and its unit normal is ( − cos θ , 0 , sin θ ) .
A matrix of unit vectors spanning the cutting plane is V , where,
V = ⎣ ⎡ 0 1 0 s 0 c ⎦ ⎤
where s = sin θ , c = c o s θ
points on the cutting plane are given by r = r 0 + V u
Let's substitute this into the equation of the cone; this will result in the equation of the points common to both the cone and the cutting plane.
( r 0 + V u ) T Q ( r 0 + V u ) = 0
expanding, this becomes,
r 0 T Q r 0 + 2 u T V T Q r 0 + u T V T Q V u = 0
Evaluating the above expression, term by term, we obtain,
V T Q = [ 0 s c 2 c 2 0 0 − c s 2 ]
so that,
V T Q r 0 = [ 0 s c ( r 1 c − H s ) ]
and,
V T Q V = [ c 2 0 0 0 ]
and finally, r 0 T Q r 0 = r 1 2 c 2 − s 2 H 2
so now the equation of the cut reads,
r 1 2 c 2 − s 2 H 2 + 2 u 2 s c ( r 1 c − H s ) + c 2 u 1 2 = 0
divide by c 2 , then
r 1 2 − R 2 + 2 u 2 s ( r 1 − R ) + u 1 2 = 0
and this is a parabola in the u 1 - u 2 plane with axis of symmetry extending along the u 2 -axis
Next, we want to find the area of the cut, so we have to find the limits of u1
We note that at z = H , u 2 = 0 , and subbing this in the equation of the parabola
yields u 1 = ± R 2 − r 1 2
Re-arranging the equation of the parabola, we get
u 2 = 2 s ( R − r 1 ) 1 ( u 1 2 − ( R 2 − r 1 2 ) )
The area of the cut is given by A = − ∫ u 2 d u 1
Integrating is straightforward, and we get,
Area = A ( r 1 ) = 3 s ( R − r 1 ) 2 ( R 2 − r 1 2 ) ( 3 / 2 )
Now to find the volume we have to integrate the area A ( r 1 ) d t , where d t is the infinitesimal thickness normal to the plane of the cut
d t = cos θ d r 1
The volume cut out is ,
V = ∫ r = − R r = r 1 A ( r ) cos θ d r
= 3 2 cot θ ∫ − R r 1 ( R 2 − r 2 ) ( 3 / 2 ) / ( R − r ) d r
let r = R sin t , then the integral becomes,
∫ − 2 π α R ( 1 − sin t ) R 3 cos 3 t ⋅ R cos t d t
where α = sin − 1 R r 1
Thus the volume is given by,
V = 3 2 cot θ R 3 ∫ − 2 π α ( 1 − sin t ) cos 4 t d t
but cos 4 t = ( 1 − sin 2 t ) 2 = ( 1 − sin t ) ( 1 + sin t ) ( 1 − sin 2 t )
hence, ( 1 − sin t ) cos 4 t = ( 1 + sin t ) ( 1 − sin 2 t ) = − sin 3 t − sin 2 t + sin t + 1
= 3 2 cot θ R 3 ∫ − 2 π α − sin 3 t − sin 2 t + sin t + 1 d t
But,
∫ sin 3 t d t = − cos t + 3 1 cos 3 t
∫ sin 2 t d t = 2 1 t − 4 1 sin 2 t
Hence, the volume is given by,
V = 3 2 cot θ R 3 ( cos t − 3 1 cos 3 t − 2 1 t + 4 1 sin 2 t − cos t + t ) ∣ − π / 2 α = 2 1 ⋅ 3 1 π R 2 H
Noting that cot θ R 3 = H R 2 , we get,
3 2 ( − 3 1 cos 3 t + 2 1 t + 4 1 sin 2 t ) ∣ − π / 2 α = 6 π
Evaluating the expression between the two limits, we end up with,
3 2 ( − 3 1 cos 3 α + 2 1 α + 4 1 sin 2 α + 4 π ) = 6 π
so that,
− 3 1 cos 3 α + 2 1 α + 4 1 sin 2 α = 0
Solving this equation by numerical methods, yields, α = 0 . 2 9 9 5 5 5
Hence, r 1 = R sin α = 0 . 2 9 5 0 9 5 4 4 R
Therefore, the required length is r 1 − ( − R ) = 1 . 2 9 5 0 9 5 4 4 R = 1 . 2 9 5 0 9 5 4 4 ( 5 ) = 6 . 4 7 5