Cutting a crystal
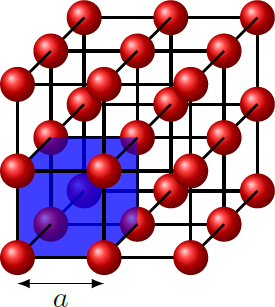
Assume we have a crystal, which is made up of only one type of atom and has a primitive cubic structure. The unit cell of the crystal is a cube with edge length . Each unit cell contains only a single atom. Each atom has a chemical bond to all the nearest neighbors that are at a distance of There are no other bonds.
Along which crystallographic plane is it easiest to cleave this crystal?
When the crystal is cut, chemical bonds must be broken. For every broken bond, a certain energy, the binding energy, has to be supplied. We are now looking for the plane for which the binding energy per surface area is the smallest.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
We consider the surfaces that result when the crystal is cleaved.
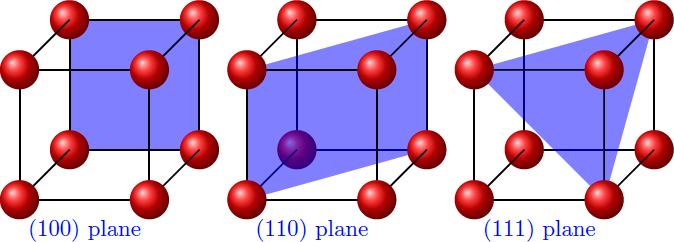
The (100) plane is a quadratic lattice with edge length a . At the (110) plane, we get a rectangular grid in which the long side is the face diagonals of unit cube, 2 a . In the case of the (111) plane, however, we have a hexagonal lattice consisting of equilateral triangles with the edge length 2 a .
In complete crystal, each atom has N = 6 nearest neighbors and hence N chemical bonds. Within the surface, each atom has k chemical bonds. The remaining N − k bonds must therefore each be below the surface or are broken. Since the surface in the complete crystal is a mirror plane, the number of broken bonds per surface atom is just b = 2 1 ( N − k ) . If every atom on the surface occupies an area A , the number of broken bonds per surface area is σ = surface area number of broken bonds = A b = 2 A N − k The area A represents the area of the parallelogram corresponding to the unit cell of the two-dimensional lattice at the surface.
This bond density σ results for the different cases to σ ( 1 0 0 ) σ ( 1 1 0 ) σ ( 1 1 1 ) = 2 ⋅ a 2 6 − 4 = a 2 1 = 2 ⋅ ( a ⋅ 2 a ) 6 − 2 = a 2 2 ≈ 1 . 4 1 ⋅ a 2 1 = 2 ⋅ ( 2 a ⋅ 2 3 a ) 6 − 0 = a 2 3 ≈ 1 . 7 3 ⋅ a 2 1 Thus, the simplest way to cleave the crystal is along the (100) plane, since the fewest bonds must be broken here.