Cutting A Cylinder

Geometry Level 4

Suppose you have a toilet roll tube. (Just the little cardboard part that's left over once you run out of toilet paper) And, just for fun, you decide to flatten it out and cut a straight diagonal line across it. So, while it's flat it looks like this:

Then you push it back out into a shape of a circular cylinder.

When you are done, if you stand it up vertically and look sideways at it with the tallest part on the right and the shortest part on the left, qualitatively which of the following will it look most like?

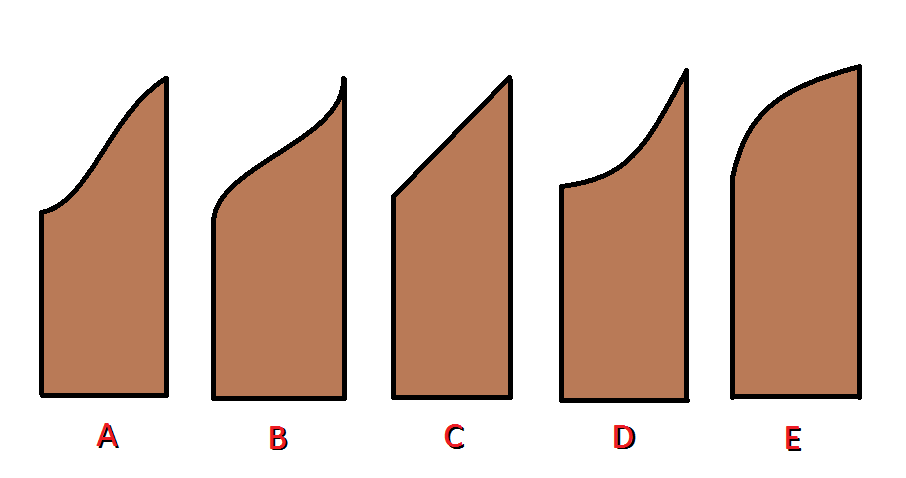
And, be honest, how many of you tried cutting one up to answer this question? ;^)

A B C D E None of these

1 solution

Geoff Pilling
Jul 14, 2016

If you do the math (or try cutting one up next time you get a chance! ;) ) you'll find that it actually forms a perfect inverse sinusoid, resembling $\boxed{B}$

Just for fun, I cut up one of my own... Not a great photo, but shows the curvature of the cut which was straight when it was flat...

I have used all my toilet paper to answer this question :)

Hải Trung Lê - 4 years, 11 months ago

Hahahahaha... ;)

Geoff Pilling - 4 years, 10 months ago

Can you provide the intuition for why this is happening?

Simply put, when flat, the rate of change if height with respect to horizontal distance is a constant. However, when curved into a cylinder, the ends get compressed more, and so there is an increase in the rate of change. This is essentially related rates applied to the real world :)

Calvin Lin Staff - 4 years, 10 months ago

Sadly, my imagination has failed me. I answered E because it was closest to my mental image of what would happen.

Manuel Kahayon - 4 years, 11 months ago

Isn't it an inverse sine function?

Ferran Espuña - 4 years, 11 months ago

Yes it is! I've updated the solution accordingly...

Geoff Pilling - 4 years, 11 months ago

I thought it would look like a spiral from sideways. And, the portion that I would see must be something like an odd function. The option B fulfilled that criteria.

Atomsky Jahid - 4 years, 10 months ago

I answered B for the same reason

Z G - 2 years, 9 months ago

That's so weird

David Pilling - 4 years, 11 months ago

..what, after you turn the tube? Sometimes a straight diagonal can still look like a straight diagonal cross section. This question is suspect to multiple answers

Mathew Korbin - 4 years, 11 months ago

There... I've clarified the description a bit so there can be only one way you are looking at it.

Geoff Pilling - 4 years, 11 months ago

If you flatten the cylinder you get a rectangle, which is equivalent to the cylinder's side view. Hence if you cut a straight diagonal while it's flat, you'll get the same thing in the cylinder's side view. Otherwise 90 degree elbows used in piping that are made up of two tubes with a 45 degree cut wouldn't work. The answer to this problem is C.

Jesus Leon - 4 years, 11 months ago

Ah, yeah, its not that intuitive...

I agree that both side views are rectangular, but, due to the curvature of the tube, when you reshape the tube back into a cylinder, your cut is no longer straight but "morphs" into the shape of a sinusoid... :) Try it out on an old toilet paper roll and you'll see...

I've added a picture in the solution of one I cut up of my own...

Geoff Pilling - 4 years, 11 months ago

Cutting A Cylinder

And, be honest, how many of you tried cutting one up to answer this question? ;^)

1 solution

0 pending reports