Cutting a Dodecahedron in Half

Geometry Level 2

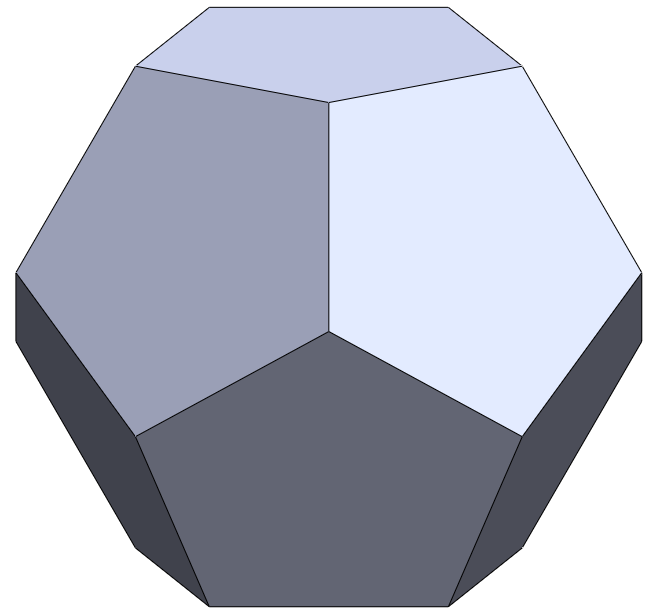
A dodecahedron is shown in the image below resting on one its faces. If we were to pass a horizontal plane half-way between the lower base and upper base, the intersection will be a regular decagon (10-gon). Find the ratio of the side length of this decagon to the edge length of the dodecahedron.

cos ⁡ 5 4 ∘ \cos 54^{\circ} sin ⁡ 10 8 ∘ \sin 108^{\circ} sin ⁡ 5 4 ∘ \sin 54^{\circ} cos ⁡ 10 8 ∘ \cos 108^{\circ}

Hosam Hajjir by Hosam Hajjir , 56, Canada

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

Zico Quintina
May 6, 2018

A side of the decagon is the segment joining the midpoints of two adjacent edges of one of the side pentagonal faces of the dodecahedron.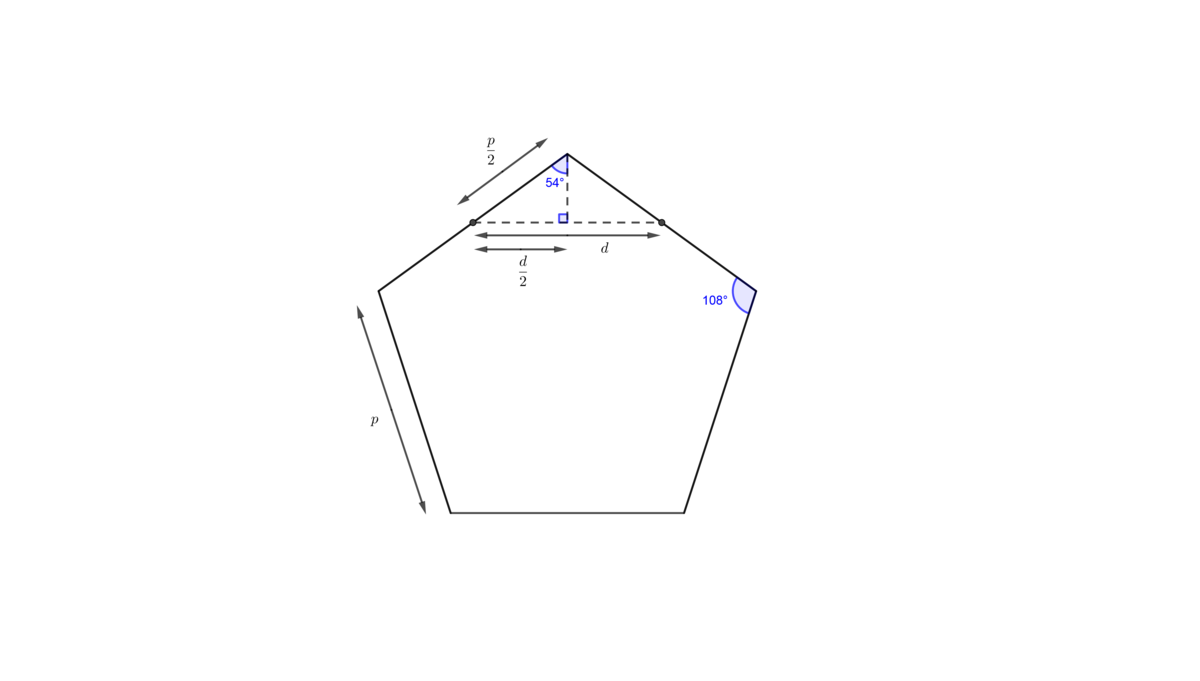 Referring to the above diagram, the ratio in question is d p = d 2 p 2 = sin ⁡ 5 4 ∘ \dfrac{d}{p} = \dfrac{\frac{d}{2}}{\frac{p}{2}} = \boxed{ \sin 54^{\circ}}

2 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...