Cutting a Parabolic Region in Half
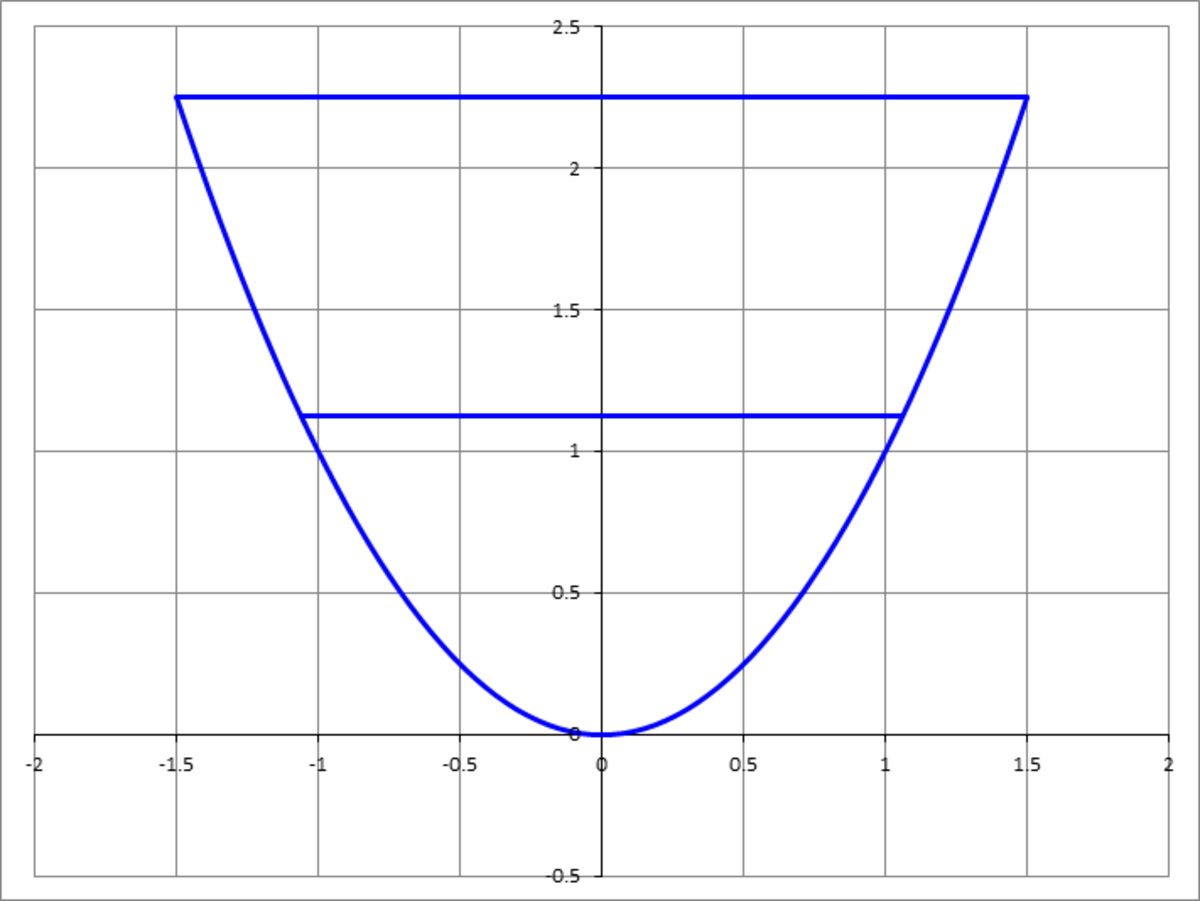
A parabolic region is bounded by the curve y = a x 2 , and y = b . Where should we draw a horizontal line that will cut this region by half ? If the horizontal line is y = c , find c .
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
From the given conditions of the problem we get ∫ 0 b y d y = 2 ∫ 0 c y d y ⟹ b 2 3 = 2 c 2 3 ⟹ c = 2 − 3 2 b .
The line and curve y = b and y = a x 2 intersect at ( ± a b , b ) , and since the area of a parabola is 3 2 the area of its inscribed rectangle, the area of the large parabola is A L = 3 2 ⋅ 2 a b ⋅ b = 3 a 4 b b .
Similarly, the area of the small parabola bounded by y = c and y = a x 2 is A S = 3 a 4 c c .
To cut the region in half, 2 A S = A L , or 2 3 a 4 c c = 3 a 4 b b , and this solves to c = 2 − 3 2 b .