Cutting a Paraboloid According to Specs
A paraboloid (shown below) is described by .
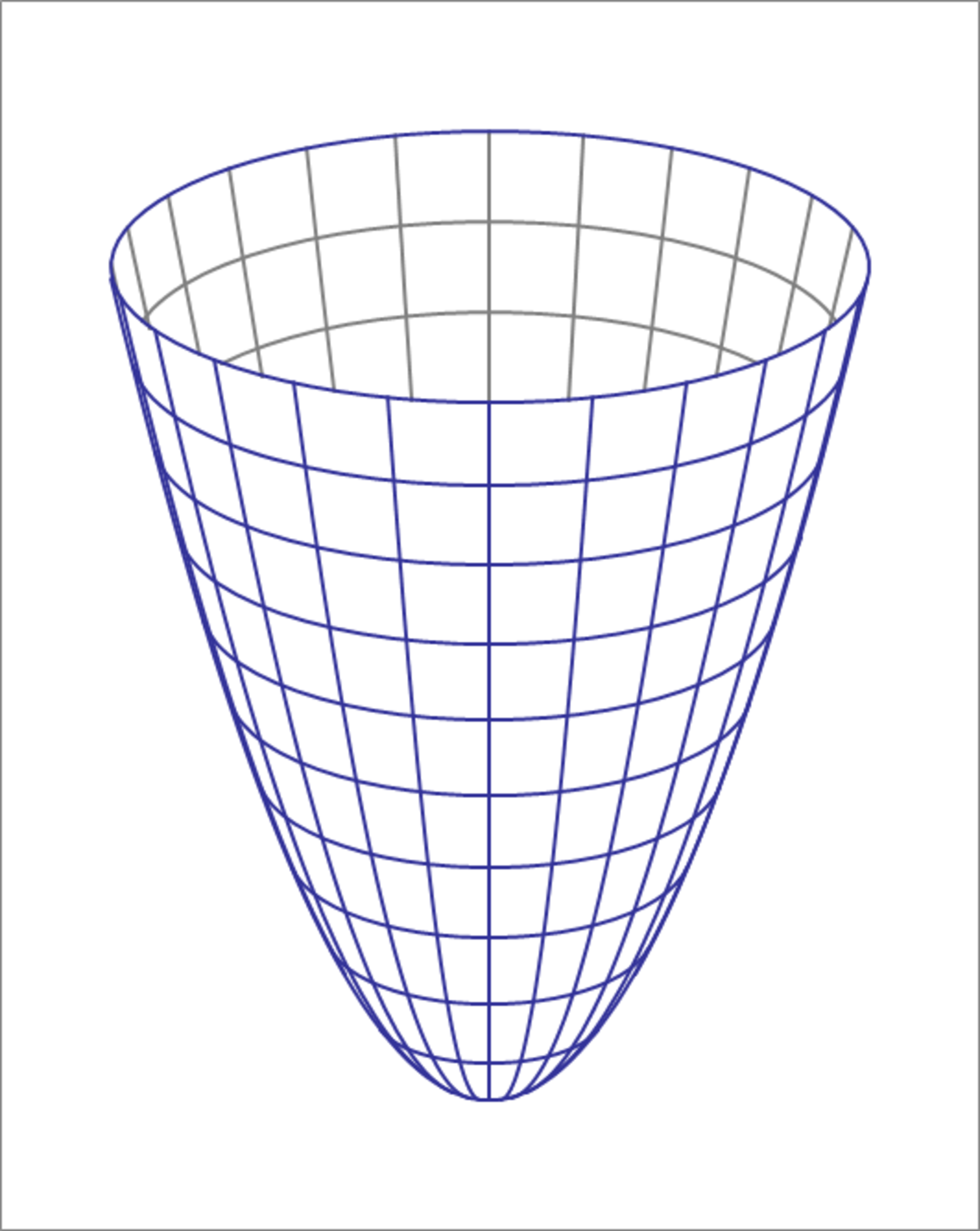
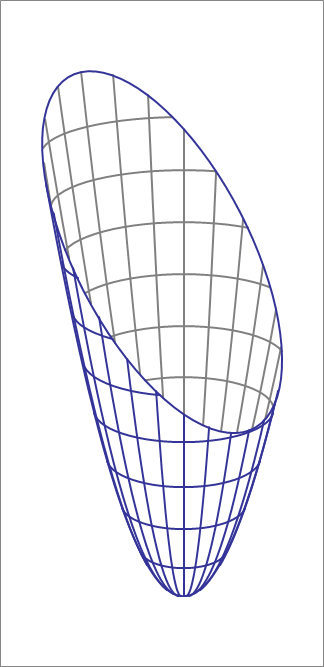
It is to be cut by a plane so that the resulting cut boundary is an ellipse with semi-major and semi-minor axes of 5 and 3 units. If is the angle that this plane's normal makes with the -axis, and is the -intercept of the plane, then find and .
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The equation of the paraboloid can be written as,
x 2 + y 2 − z = 0
So, if we define r = ( x , y , z ) then we can write the paraboloid equation as,
r T Q r + b T r = 0
where,
Q = ⎣ ⎡ 1 0 0 0 1 0 0 0 0 ⎦ ⎤ and b = ⎣ ⎡ 0 0 − 1 ⎦ ⎤
Since the paraboloid is symmetrical about the z-axis, we can, without loss of generality, take the normal of the plane, to lie in the x z -plane. If the angle it makes with the z -axis is ϕ , then the unit normal vector can be taken as,
n ^ = ( − sin ϕ , 0 , cos ϕ )
Orthogonal to the above defined normal and orthogonal to each other are these two unit vectors
u 1 = ( cos ϕ , 0 , sin ϕ ) T u 2 = ( 0 , 1 , 0 ) T
If we define the 3 × 2 matrix V = [ u 1 , u 2 ] , then any point on the plane, can be expressed as,
r = r 0 + V u
where r 0 is any fixed point on the plane, and for convenience we'll take it as the z -intercept of the plane, that is,
we'll take r 0 = ( 0 , 0 , z 0 ) T . (Remember, all vectors are considered column vectors). The 2 × 1 vector u multiplying V is the coordinate of the point r with respect to the two axes u 1 and u 2 .
Substituting the expression for points on the plane into the equation of the paraboloid gives us
( r 0 + V u ) T Q ( r 0 + V u ) + b T ( r 0 + V u ) = 0
Expanding,
u T V T Q V u + 2 u T V T Q r 0 + r 0 T Q r 0 + b T r 0 + u T V T b = 0
Now, we'll evaluate each of these terms.
V T Q V = [ cos ϕ 0 0 1 sin ϕ 0 ] ⎣ ⎡ 1 0 0 0 1 0 0 0 0 ⎦ ⎤ ⎣ ⎡ cos ϕ 0 sin ϕ 0 1 0 ⎦ ⎤ = [ cos ϕ 0 0 1 0 0 ] ⎣ ⎡ cos ϕ 0 sin ϕ 0 1 0 ⎦ ⎤ = [ cos 2 ϕ 0 0 1 ]
V T Q r 0 = [ cos ϕ 0 0 1 0 0 ] ⎣ ⎡ 0 0 z 0 ⎦ ⎤ = [ 0 0 ]
r 0 T Q r 0 = [ 0 0 z 0 ] ⎣ ⎡ 1 0 0 0 1 0 0 0 0 ⎦ ⎤ ⎣ ⎡ 0 0 z 0 ⎦ ⎤ = 0
b T r 0 = [ 0 0 − 1 ] ⎣ ⎡ 0 0 z 0 ⎦ ⎤ = − z 0
V T b = [ cos ϕ 0 0 1 sin ϕ 0 ] ⎣ ⎡ 0 0 − 1 ⎦ ⎤ = [ − sin ϕ 0 ]
So the equation of the cut is as follows:
u T ( V T Q V ) u + u T V T b = z 0
We next introduce the vector u 0 defined as follows,
u 0 = − 2 1 ( V T Q V ) − 1 V T b = − 2 1 [ cos 2 ϕ 1 0 0 1 ] [ − sin ϕ 0 ] = 2 1 [ cos 2 ϕ sin ϕ 0 ]
Then, we can write now write the equation of the cut as,
( u − u 0 ) T V T Q V ( u − u 0 ) = z 0 + u 0 T ( V T Q V ) u 0
Evaluating the rightmost term, results in,
( u − u 0 ) T ( V T Q V ) ( u − u 0 ) = z 0 + 4 1 tan 2 ϕ
Dividing by the right hand side, we obtain
( u − u 0 ) T Q 1 ( u − u 0 ) = 1
where
Q 1 = ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ z 0 + 4 1 tan 2 ϕ cos 2 ϕ 0 0 z 0 + 4 1 tan 2 ϕ 1 ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤
Now we can compare this form to the equation of an ellipse with semi-major and semi-minor axes a and b which is given by:
w T D w = 1 where
D = ⎣ ⎢ ⎡ a 2 1 0 0 b 2 1 ⎦ ⎥ ⎤
Comparing the two matrices Q 1 and D , we deduce that,
a b = cos ϕ and that b 2 = z 0 + 4 1 tan 2 ϕ
Therefore,
cos ϕ = 5 3 = 0 . 6 and z 0 = 9 − 4 1 9 1 6 = 9 − 9 4 = 9 7 7