Cutting a pyramid in half
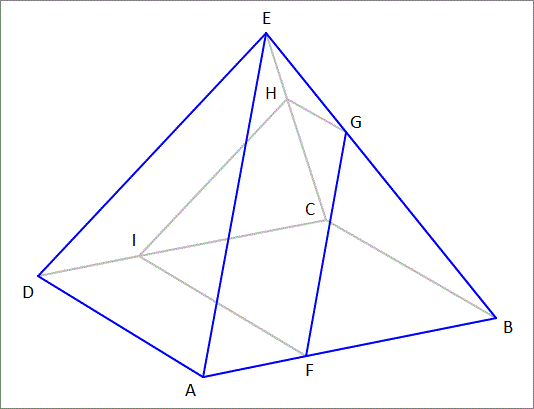
A right pyramid A B C D E has a square base A B C D of side length 1 2 . The pyramid height is 1 0 . You want to cut it in two equal halves (by volume) by passing a cutting plane parallel to one of the pyramid's triangular faces, as shown in the figure. Find the length of F B .
The answer is 7.832.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Let x = F B and y = H G and draw the following segments as follows:
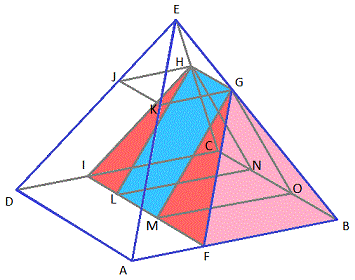
Since A B = 1 2 and F B = x , y = H G = K G = A F = A B − F B = 1 2 − x .
The lower half of the cut solid is made up of on triangular prism G M O H L N (in blue) and two congruent pyramids H L N C I and G M O B F (in red), and the two pyramids can be combined to make a single pyramid that is similar to the original pyramid. Since they are similar and the original pyramid has a side length of 1 2 and a height of 1 0 , the red pyramid has a height of h = 1 2 1 0 x = 6 5 x .
Since the original pyramid is cut in half by volume, 2 1 V orig pyr = V red pyr + V blue prism , or 2 1 ⋅ 3 1 1 2 2 1 0 = 3 1 x 2 h + 2 1 x h y , or 2 4 0 = 3 1 x 2 ( 6 5 x ) + 2 1 x ( 6 5 x ) ( 1 2 − x ) , which rearranges to x 3 − 3 6 x 2 + 1 7 2 8 = 0 , and has a solution of x ≈ 7 . 8 3 2 for 0 < x < 1 2 .
Let x = F B , then the coordinates of points G , H are
G = ( 1 2 − 2 1 x , 2 1 x , 2 1 x tan θ )
H = ( 1 2 − 2 1 x , 1 2 − 2 1 x , 2 1 x tan θ )
where θ is the angle between the base and a triangular face.
The volume is,
V = 2 1 ( x ) ( 1 2 − x ) ( 2 1 x tan θ ) + 3 2 ( x ) ( 2 1 x ) ( 2 1 x tan θ ) ) = 2 1 3 1 ( 1 2 2 ) ( 1 0 )
Multiply through by 1 2 / tan θ , and noting that tan θ = 3 5 ,then the equation becomes,
3 x 2 ( 1 2 − x ) + 2 x 3 = 1 2 ( 2 4 0 ) ( 3 / 5 ) = 1 7 2 8
or
x 3 − 3 6 x 2 + 1 7 2 8 = 0
Solving this cubic equation gives the result of x = 7 . 8 3 2