Cutting a Quarter Circular Region by Half
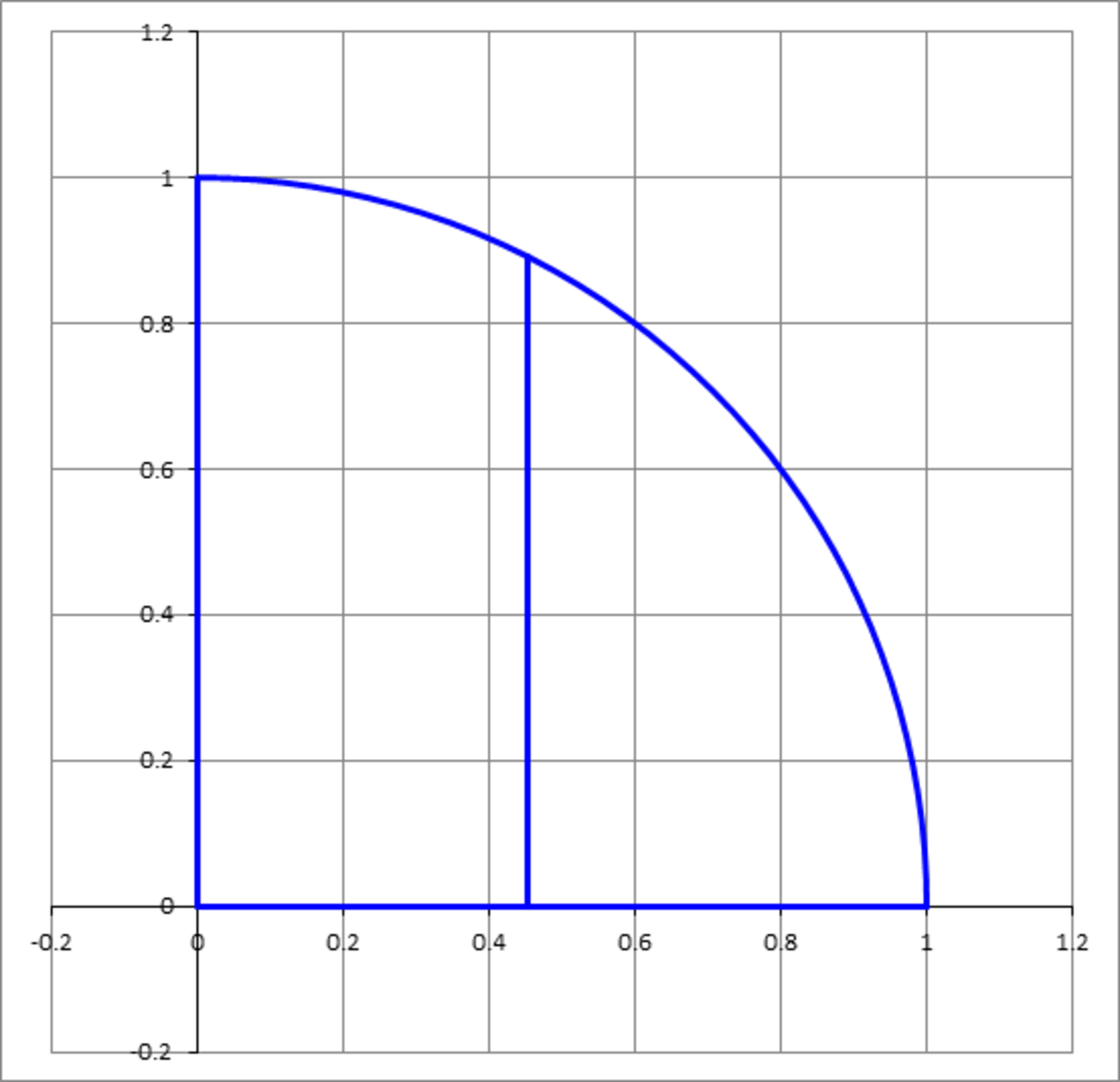
A quarter circle of radius , in the first quadrant is depicted in the figure below. We want to divide the region in two halves by area, by passing a vertical line . Find .
Note:
Image below is not drawn to scale.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Reflect the quarter circle and label it as follows:
Then the area of the sector enclosed by A O B is A S = 2 π θ ⋅ π r 2 = 2 θ , and the area of △ A O B is A T = 2 1 r 2 sin θ = 2 1 sin θ . The difference between these two areas must equal half the area of the semicircle A O = 2 1 π r 2 = 2 1 π , so A S − A T = 2 1 A O or 2 θ − 2 1 sin θ = 2 1 ⋅ 2 1 π , which solves numerically to θ ≈ 2 . 3 0 9 9 .
From △ A O C , x = cos 2 θ , and substituting the value of θ from above gives x ≈ cos 2 2 . 3 0 9 9 ≈ 0 . 4 0 4 .