Cutting a regular dodecahedron in half - Part 2
A regular dodecahedron with unit edge length is positioned such that the line joining two opposite vertices is vertical. Then a horizontal cutting plane is passed through the center of the dodecahedron thus halving it. The cut results in a cut face that is a regular hexagon. Find the side length of this hexagon.
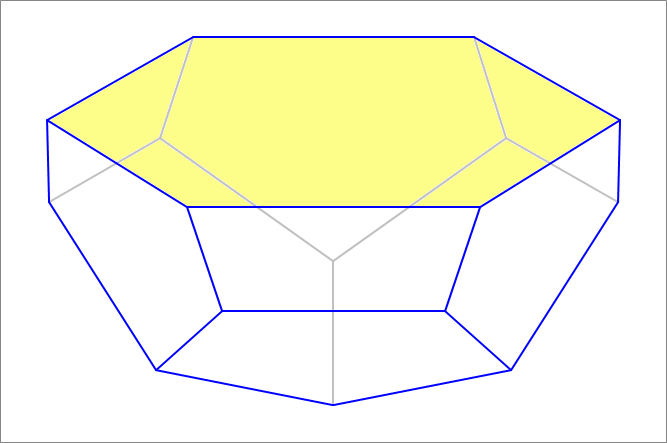
The answer is 1.309.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
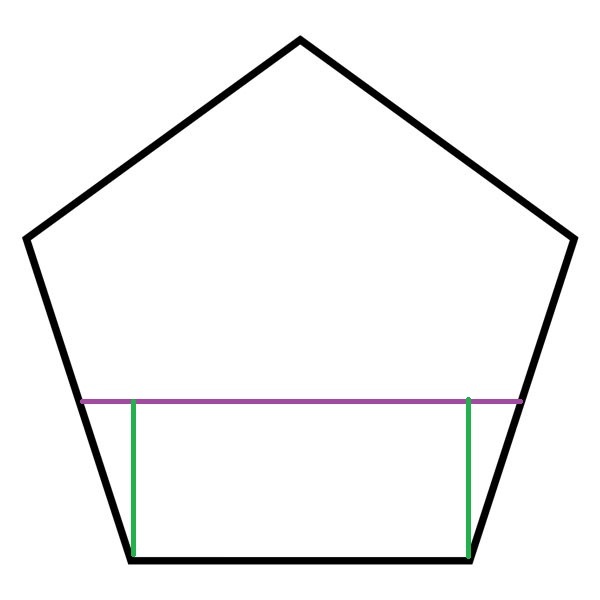
One side of the hexagon is the midsegment of the isosceles trapezoid formed by three sides of a pentagon and one diagonal.
Since the side of the pentagon is 1 and the diagonal of the pentagon is 2 1 + 5 , the midsegment (and the side of the hexagon) is the average of these two sides, which is 4 3 + 5 ≈ 1 . 3 0 9 .